Dyadic product
Encyclopedia
In mathematics
, in particular multilinear algebra
, the dyadic product
of two vectors,
and 
, each having the same dimension, is the tensor product
of the vectors and results in a tensor
of order two and rank one. It is also called outer product
.
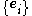, the components 
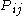of the dyadic product 
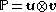may be defined by
,
where
,
,
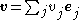and
.
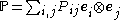obtained by multiplying
as a column vector by 
as a row vector. For example,
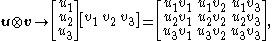
where the arrow indicates that this is only one particular representation of the dyadic product, referring to a particular basis
. In this representation, the dyadic product is a special case of the Kronecker product
.
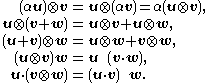
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, the dyadic product
of two vectors,
and , each having the same dimension, is the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of the vectors and results in a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of order two and rank one. It is also called outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
.
Components
With respect to a chosen basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
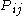, the components of the dyadic product 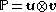may be defined by ,where
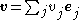, ,and
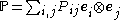.Matrix representation
The dyadic product can be simply represented as the square matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
obtained by multiplying
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
as a column vector by as a row vector. For example,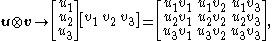where the arrow indicates that this is only one particular representation of the dyadic product, referring to a particular basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. In this representation, the dyadic product is a special case of the Kronecker product
Kronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
.
Identities
The following identities are a direct consequence of the definition of the dyadic product: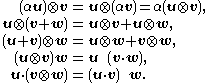See also
- DyadicsDyadicsDyadics are mathematical objects, representing linear functions of vectors. Dyadic notation was first established by Gibbs in 1884.-Definition:Dyad A is formed by two vectors a and b...
- Dyadic tensorDyadic tensorIn multilinear algebra, a dyadic is a second rank tensor written in a special notation, formed by juxtaposing pairs of vectors, along with a notation for manipulating such expressions analogous to the rules for matrix algebra....
- Tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
- Kronecker productKronecker productIn mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
- Outer productOuter productIn linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...