Essentially surjective functor
Encyclopedia
In category theory
, a functor
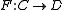
is essentially surjective (or dense) if each object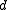
of 
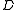is isomorphic to an object of the form 
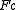for some object 
of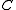 
. Any functor which is part of an equivalence
is essentially surjective.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
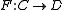
is essentially surjective (or dense) if each object
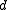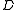of is isomorphic to an object of the form 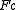for some object of 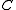. Any functor which is part of an equivalenceEquivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
is essentially surjective.