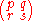In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, an elliptic function is a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 defined on the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 that is periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

 in two directions (a doubly periodic function) and at the same time is meromorphic. Historically, elliptic functions were discovered as inverse function

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

s of elliptic integral

Elliptic integral

In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...

s; these in turn were studied in connection with the problem of the arc length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

 of an ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

, whence the name derives.

Definition

Formally, an elliptic function is a meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

 f defined on C for which there exist two non-zero complex numbers a and b with a/b not real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

, such that

f(z + a) = f(z + b) = f(z)   for all z in C

wherever f(z) is defined. From this it follows that

f(z + ma + nb) = f(z)   for all z in C and all integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s m and n.

There are two methods of constructing 'canonical' elliptic functions: those of Jacobi

Carl Gustav Jakob Jacobi

Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...

 and Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

. In the theory, modern authors mostly follow Karl Weierstrass: the notations of Weierstrass's elliptic functions

Weierstrass's elliptic functions

In mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass...

 based on his -function are convenient, and any elliptic function can be expressed in terms of these. However it is the functions of Jacobi that appear most commonly in practical
problems, especially the need to avoid complex numbers, having a mapping from real to real, where the imaginary part is unnecessary or physically insignificant. Weierstrass became interested in these functions as a student of Christoph Gudermann

Christoph Gudermann

Christoph Gudermann was born in Vienenburg. He was the son of a school teacher and became a teacher himself after studying at the University of Göttingen, where his advisor was Karl Friedrich Gauss...

, a student of Carl Friedrich Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

.

The elliptic functions

Jacobi's elliptic functions

In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...

 introduced by Jacobi, and the auxiliary theta functions (not doubly periodic), are more complicated but important both for the history and for general theory. The primary difference between these two theories is that the Weierstrass functions have second-order and higher-order poles located at the corners of the periodic lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

, whereas the Jacobi functions have simple poles. The development of the Weierstrass theory is easier to present and understand, having fewer complications.

More generally, the study of elliptic functions is closely related to the study of modular functions and modular forms, a relationship proven by the modularity theorem. Examples of this relationship include the j-invariant

J-invariant

In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...

, the Eisenstein series

Eisenstein series

Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...

 and the Dedekind eta function

Dedekind eta function

The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...

.

Properties

• Any complex number ω such that f(z + ω) = f(z) for all z in C is called a period of f. If the two periods a and b are such that any other period ω can be written as ω = ma + nb with integer
  Integer
  The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
  
  s m and n, then a and b are called fundamental periods. Every elliptic function has a fundamental pair of periods
  Fundamental pair of periods
  In mathematics, a fundamental pair of periods is an ordered pair of complex numbers that define a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined....
  
  , but this pair is not unique, as described below.

• If a and b are fundamental periods describing a lattice, then exactly the same lattice can be obtained by the fundamental periods a' and b' where a' = p a + q b and b' = r a + s b where p, q, r and s being integers satisfying p s − q r = 1. That is, the matrix

has determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 one, and thus belongs to the modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

. In other words, if a and b are fundamental periods of an elliptic function, then so are a' and b' .

• If a and b are fundamental periods, then any parallelogram
  Parallelogram
  In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
  
   with vertices z, z + a, z + b, z + a + b is called a fundamental parallelogram. Shifting such a parallelogram by integral multiples of a and b yields a copy of the parallelogram, and the function f behaves identically on all these copies, because of the periodicity.

• The number of poles in any fundamental parallelogram is finite (and the same for all fundamental parallelograms). Unless the elliptic function is constant, any fundamental parallelogram has at least one pole, a consequence of Liouville's theorem
  Liouville's theorem (complex analysis)
  In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
  
  .

• The sum of the orders of the poles in any fundamental parallelogram is called the order of the elliptic function. The sum of the residues
  Residue (complex analysis)
  In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
  
   of the poles in any fundamental parallelogram is equal to zero, so in particular no elliptic function can have order one.

• The number of zeros (counted with multiplicity) in any fundamental parallelogram is equal to the order of the elliptic function.

• The set of all elliptic functions which share some two periods form a field
  Field (mathematics)
  In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
  
  .

• The derivative
  Derivative
  In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
  
   of an elliptic function is again an elliptic function, with the same periods.

• The Weierstrass elliptic function ℘ is the prototypical elliptic function, and in fact, the field of elliptic functions with respect to a given lattice is generated by ℘ and its derivative ℘′.

See also

• Jacobi's elliptic functions
  Jacobi's elliptic functions
  In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
  
  
• Elliptic integral
  Elliptic integral
  In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
  
  
• Jacobi theta function
• Ramanujan theta function
  Ramanujan theta function
  In mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta...
  
  

External links

• Translation of Niels Abel's Research on Elliptic Functions at Convergence