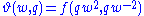Ramanujan theta function
Encyclopedia
In mathematics
, particularly q-analog
theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta. The function is named after Srinivasa Ramanujan
.
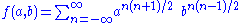
for The Jacobi triple product identity then takes the form
The Jacobi triple product identity then takes the form
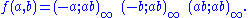
Here, the expression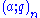 denotes the q-Pochhammer symbol. Identities that follow from this include
denotes the q-Pochhammer symbol. Identities that follow from this include

and

and
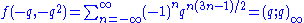
this last being the Euler function, which is closely related to the Dedekind eta function
. The Jacobi theta function may be written in terms of the nome as:
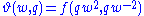
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta. The function is named after Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
.
Definition
The Ramanujan theta function is defined as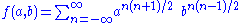
for
 The Jacobi triple product identity then takes the form
The Jacobi triple product identity then takes the form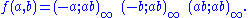
Here, the expression
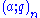 denotes the q-Pochhammer symbol. Identities that follow from this include
denotes the q-Pochhammer symbol. Identities that follow from this include
and

and
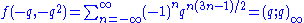
this last being the Euler function, which is closely related to the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. The Jacobi theta function may be written in terms of the nome as: