
Q-Pochhammer symbol
Encyclopedia
In mathematics
, in the area of combinatorics
, a q-Pochhammer symbol, also called a q-shifted factorial, is a q-analog
of the common Pochhammer symbol
. It is defined as
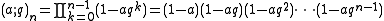
with

by definition. The q-Pochhammer symbol is a major building block in the construction of q-analogs; for instance, in the theory of basic hypergeometric series
, it plays the role that the ordinary Pochhammer symbol plays in the theory of generalized hypergeometric series.
Unlike the ordinary Pochhammer symbol, the q-Pochhammer symbol can be extended to an infinite product:

This is an analytic function
of q in the interior of the unit disk, and can also be considered as a formal power series
in q. The special case

is known as Euler's function, and is important in combinatorics
, number theory
, and the theory of modular forms.
A q-series is a series
in which the coefficients are functions of q, typically depending on q via q-Pochhammer symbols.
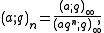
which extends the definition to negative integers n. Thus, for nonnegative n, one has
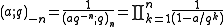
and
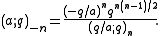
The q-Pochhammer symbol is the subject of a number of q-series identities, particularly the infinite series expansions
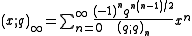
and
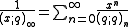 ,
,
which are both special cases of the q-binomial theorem:
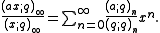
 in
in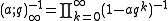
is the number of partitions of m into at most n parts.
Since, by conjugation of partitions, this is the same as the number of partitions of m into parts of size at most n, by identification of generating series we obtain the identity:
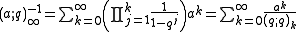
as in the above section.
We also have that the coefficient of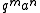 in
in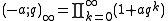
is the number of partitions of m into n or n-1 distinct parts.
By removing a triangular partition with n-1 parts from such a partition, we are left with an arbitrary partition with at most n parts. This gives a weight-preserving bijection between the set of partitions into n or n-1 distinct parts and the set of pairs consisting of a triangular partition having n-1 parts and a partition with at most n parts. By identifying generating series, this leads to the identity:
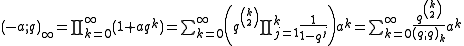
also described in the above section.
The q-binomial theorem itself can also be handled by a slightly more involved combinatorial argument of a similar flavour.

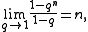
we define the q-analog of n, also known as the q-bracket or q-number of n to be

From this one can define the q-analog of the factorial
, the q-factorial, as
Again, one recovers the usual factorial by taking the limit as q approaches 1. This can be interpreted as the number of flags in an n-dimensional vector space over the field with q elements, and taking the limit as q goes to 1 yields the interpretation of an ordering on a set as a flag in a vector space over the field with one element
.
A product of negative integer q-brackets can be expressed in terms of the q-factorial as:

From the q-factorials, one can move on to define the q-binomial coefficients, also known as Gaussian coefficients, Gaussian polynomials, or Gaussian binomial coefficients:
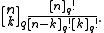
One can check that
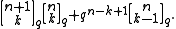
One also obtains a q-analog of the Gamma function
, called the q-gamma function
, and defined as
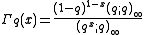
This converges to the usual Gamma function as q approaches 1 from inside the unit disc.. Note that
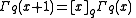
for any x and
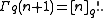
for non-negative integer values of n. Alternatively, this may be taken as an extension of the q-factorial function to the real number system.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a q-Pochhammer symbol, also called a q-shifted factorial, is a q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
of the common Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
. It is defined as
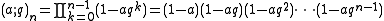
with

by definition. The q-Pochhammer symbol is a major building block in the construction of q-analogs; for instance, in the theory of basic hypergeometric series
Basic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
, it plays the role that the ordinary Pochhammer symbol plays in the theory of generalized hypergeometric series.
Unlike the ordinary Pochhammer symbol, the q-Pochhammer symbol can be extended to an infinite product:

This is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of q in the interior of the unit disk, and can also be considered as a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in q. The special case

is known as Euler's function, and is important in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and the theory of modular forms.
A q-series is a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
in which the coefficients are functions of q, typically depending on q via q-Pochhammer symbols.
Identities
The finite product can be expressed in terms of the infinite product: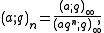
which extends the definition to negative integers n. Thus, for nonnegative n, one has
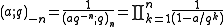
and
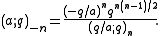
The q-Pochhammer symbol is the subject of a number of q-series identities, particularly the infinite series expansions
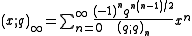
and
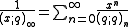 ,
,which are both special cases of the q-binomial theorem:
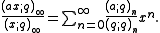
Combinatorial interpretation
The q-Pochhammer symbol is closely related to the enumerative combinatorics of partitions. The coefficient of in
in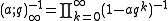
is the number of partitions of m into at most n parts.
Since, by conjugation of partitions, this is the same as the number of partitions of m into parts of size at most n, by identification of generating series we obtain the identity:
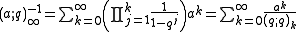
as in the above section.
We also have that the coefficient of
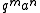 in
in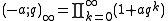
is the number of partitions of m into n or n-1 distinct parts.
By removing a triangular partition with n-1 parts from such a partition, we are left with an arbitrary partition with at most n parts. This gives a weight-preserving bijection between the set of partitions into n or n-1 distinct parts and the set of pairs consisting of a triangular partition having n-1 parts and a partition with at most n parts. By identifying generating series, this leads to the identity:
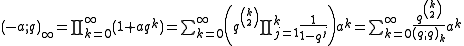
also described in the above section.
The q-binomial theorem itself can also be handled by a slightly more involved combinatorial argument of a similar flavour.
Multiple arguments convention
Since identities involving q-Pochhammer symbols so frequently involve products of many symbols, the standard convention is to write a product as a single symbol of multiple arguments:
Relationship to other q-functions
Noticing that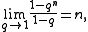
we define the q-analog of n, also known as the q-bracket or q-number of n to be

From this one can define the q-analog of the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
, the q-factorial, as
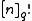 |
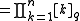 |
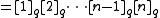 |
|
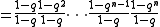 |
|
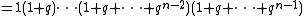 |
|
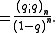 |
Again, one recovers the usual factorial by taking the limit as q approaches 1. This can be interpreted as the number of flags in an n-dimensional vector space over the field with q elements, and taking the limit as q goes to 1 yields the interpretation of an ordering on a set as a flag in a vector space over the field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
.
A product of negative integer q-brackets can be expressed in terms of the q-factorial as:

From the q-factorials, one can move on to define the q-binomial coefficients, also known as Gaussian coefficients, Gaussian polynomials, or Gaussian binomial coefficients:
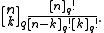
One can check that
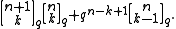
One also obtains a q-analog of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, called the q-gamma function
Q-gamma function
In q-analog theory, the q-gamma function, or basic gamma function, is a generalization of the ordinary Gamma function closely related to the double gamma function. It was introduced by...
, and defined as
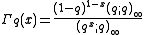
This converges to the usual Gamma function as q approaches 1 from inside the unit disc.. Note that
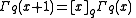
for any x and
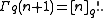
for non-negative integer values of n. Alternatively, this may be taken as an extension of the q-factorial function to the real number system.
See also
- Basic hypergeometric seriesBasic hypergeometric seriesIn mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
- Pochhammer symbolPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
- Q-derivativeQ-derivativeIn mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration-Definition:...
- Q-theta function
- Elliptic gamma function
- Jacobi theta function

