In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the open unit disk (or disc) around P (where P is a given point in the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

), is the set of points whose distance from P is less than 1:


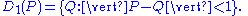
The closed unit disk around P is the set of points whose distance from P is less than or equal to one:


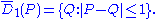
Unit disks are special cases of disks

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

 and unit balls.

Without further specifications, the term unit disk is used for the open unit disk about the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

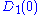, , with respect to the standard Euclidean metric

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

. It is the interior of a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 of radius 1, centered at the origin. This set can be identified with the set of all complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s of absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

 less than one. When viewed as a subset of the complex plane (C), the unit disk is often denoted .

The open unit disk, the plane, and the upper half-plane

The function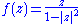


is an example of a real analytic

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

 and bijective function from the open unit disk to the plane; its inverse function is also analytic. Considered as a real 2-dimensional analytic manifold

Analytic manifold

In mathematics, an analytic manifold is a topological manifold with analytic transition maps. Every complex manifold is an analytic manifold....

, the open unit disk is therefore isomorphic to the whole plane. In particular, the open unit disk is homeomorphic to the whole plane.

There is however no conformal

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

 bijective map between the open unit disk and the plane. Considered as a Riemann surface

Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...

, the open unit disk is therefore different from the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

.

There are conformal bijective maps between the open unit disk and the open upper half-plane. So considered as a Riemann surface, the open unit disk is isomorphic ("biholomorphic", or "conformally equivalent") to the upper half-plane, and the two are often used interchangeably.

Much more generally, the Riemann mapping theorem states that every simply connected open subset

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 of the complex plane that is different from the complex plane itself admits a conformal and bijective map to the open unit disk.

One bijective conformal map from the open unit disk to the open upper half-plane is the Möbius transformation
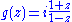  which is the inverse of the Cayley transform.

Geometrically, one can imagine the real axis being bent and shrunk so that the upper half-plane becomes the disk's interior and the real axis forms the disk's circumference, save for one point at the top, the "point at infinity". A bijective conformal map from the open unit disk to the open upper half-plane can also be constructed as the composition of two stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

s: first the unit disk is stereographically projected upward onto the unit upper half-sphere, taking the "south-pole" of the unit sphere as the projection center, and then this half-sphere is projected sideways onto a vertical half-plane touching the sphere, taking the point on the half-sphere opposite to the touching point as projection center.

The unit disk and the upper half-plane are not interchangeable as domains for Hardy spaces. Contributing to this difference is the fact that the unit circle has finite (one-dimensional) Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

 while the real line does not.

Hyperbolic space

The open unit disk is commonly used as a model for the hyperbolic plane

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

, by introducing a new metric on it, the Poincaré metric

Poincaré metric

In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...

. Using the above mentioned conformal map between the open unit disk and the upper half-plane, this model can be turned into the Poincaré half-plane model

Poincaré half-plane model

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....

 of the hyperbolic plane. Both the Poincaré disk and the Poincaré half-plane are conformal models of hyperbolic space, i.e. angles measured in the model coincide with angles in hyperbolic space, and consequently the shapes (but not the sizes) of small figures are preserved.

Another model of hyperbolic space is also built on the open unit disk: the Klein model

Klein model

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...

. It is not conformal, but has the property that straight lines in the model correspond to straight lines in hyperbolic space.

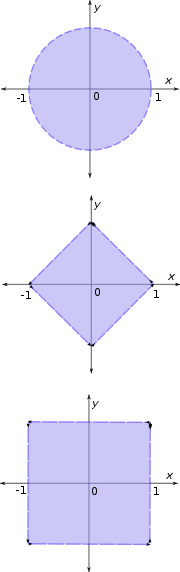
Unit disks with respect to other metrics

One also considers unit disks with respect to other metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

s. For instance, with the taxicab metric

Taxicab geometry

Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...

 and the Chebyshev metric

Chebyshev distance

In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...

 disks look like squares (even though the underlying topologies

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 are the same as the Euclidean one).

The area of the Euclidean unit disk is π and its perimeter

Perimeter

A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...

 is 2π. In contrast, the perimeter (relative to the taxicab metric) of the unit disk in the taxicab geometry is 8. In 1932, Stanisław Gołąb proved that in metrics arising from a norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

, the perimeter of the unit disk can take any value in between 6 and 8, and that these extremal values are obtained if and only if the unit disk is a regular hexagon or a parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

, respectively.

External links

• On the Perimeter and Area of the Unit Disc, by J.C. Álvarez Pavia and A.C. Thompson