Riemann mapping theorem
Encyclopedia
In complex analysis
, the Riemann mapping theorem states that if
is a non-empty simply connected
open subset
of the complex number plane
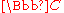which is not all of 
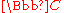, then there exists a biholomorphic
(bijective and holomorphic
) mapping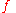
from 
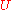onto the open unit disk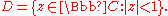
This mapping is known as a Riemann mapping.
Intuitively, the condition that
be simply connected means that 
does not contain any “holes”. The fact that 
is biholomorphic implies that it is a conformal map
and therefore angle-preserving. Intuitively, such a map preserves the shape of any sufficiently small figure, while possibly rotating and scaling (but not reflecting) it.
Henri Poincaré
proved that the map
is essentially unique: if 
is an element of 
and φ is an arbitrary angle, then there exists precisely one 
as above with the additional properties that 
maps 
into 
and that the argument of the derivative of 
at the point 
is equal to φ. This is an easy consequence of the Schwarz lemma
.
As a corollary of the theorem, any two simply connected open subsets of the Riemann sphere
(which each lack at least two points of the sphere) can be conformally mapped into each other (because conformal equivalence is an equivalence relation).
of
is piecewise smooth) by Bernhard Riemann
in 1851 in his PhD thesis. Lars Ahlfors wrote once, concerning the original formulation of the theorem, that it was “ultimately formulated in terms which would defy any attempt of proof, even with modern methods”. Riemann's flawed proof depended on the Dirichlet principle (whose name was created by Riemann himself), which was considered sound at the time. However, Karl Weierstraß
found that this principle was not universally valid. Later, David Hilbert
was able to prove that, to a large extent, the Dirichlet principle is valid under the hypothesis that Riemann was working with. However, in order to be valid, the Dirichlet principle needs certain hypotheses concerning the boundary of
which are not valid for simply connected domains in general. Simply connected domains with arbitrary boundaries were first treated by .
The first proof of the theorem is due to Constantin Carathéodory
, who published it in 1912. His proof used Riemann surface
s and it was simplified by Paul Koebe
two years later in a way which did not require them.
Another proof, due to Leopold Fejér
and to Frigyes Riesz
, was published in 1922 and it was rather shorter than the previous ones. In this proof, like in Riemann's proof, the desired mapping was obtained as the solution of an extremal problem. The Fejér-Riesz proof was further simplified by Alexander Ostrowski and by Carathéodory.
and 
, we want to construct a function 
which maps 
to the unit disk and 
to 
. For this sketch, we will assume that 
is bounded and its boundary is smooth, much like Riemann did. Write
where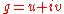
is some (to be determined) holomorphic function with real part 
and imaginary part 
. It is then clear that z0 is the only zero of f. We require 
for 
on the boundary of 
, so we need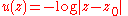
on the boundary. Since
is the real part of a holomorphic function, we know that 
is necessarily a harmonic function
, i.e. it satisfies Laplace's equation
.
The question then becomes: does a real-valued harmonic function
exist that is defined on all of 
and has the given boundary condition? The positive answer is provided by the Dirichlet principle. Once the existence of u has been established, the Cauchy-Riemann equations
for the holomorphic function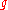
allow us to find 
(this argument depends on the assumption that 
be simply connected). Once 
and 
have been constructed, one has to check that the resulting function 
does indeed have all the required properties.
s: If U is a simply-connected open subset of a Riemann surface
, then U is biholomorphic to one of the following: the Riemann sphere
, the complex plane
or the open unit disk. This is known as the uniformization theorem
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Riemann mapping theorem states that if
is a non-empty simply connectedSimply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the complex number plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
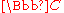which is not all of 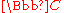, then there exists a biholomorphicBiholomorphy
In the mathematical theory of functions of one or more complex variables, and also in complex algebraic geometry, a biholomorphism or biholomorphic function is a bijective holomorphic function whose inverse is also holomorphic....
(bijective and holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
) mapping
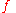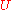from onto the open unit disk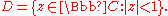This mapping is known as a Riemann mapping.
Intuitively, the condition that
be simply connected means that does not contain any “holes”. The fact that is biholomorphic implies that it is a conformal mapConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
and therefore angle-preserving. Intuitively, such a map preserves the shape of any sufficiently small figure, while possibly rotating and scaling (but not reflecting) it.
Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
proved that the map
is essentially unique: if is an element of and φ is an arbitrary angle, then there exists precisely one as above with the additional properties that maps into and that the argument of the derivative of at the point is equal to φ. This is an easy consequence of the Schwarz lemmaSchwarz lemma
In mathematics, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis about holomorphic functions from the open unit disk to itself. The lemma is less celebrated than stronger theorems, such as the Riemann mapping theorem, which it helps to prove...
.
As a corollary of the theorem, any two simply connected open subsets of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(which each lack at least two points of the sphere) can be conformally mapped into each other (because conformal equivalence is an equivalence relation).
History
The theorem was stated (under the assumption that the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of
is piecewise smooth) by Bernhard RiemannBernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in 1851 in his PhD thesis. Lars Ahlfors wrote once, concerning the original formulation of the theorem, that it was “ultimately formulated in terms which would defy any attempt of proof, even with modern methods”. Riemann's flawed proof depended on the Dirichlet principle (whose name was created by Riemann himself), which was considered sound at the time. However, Karl Weierstraß
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
found that this principle was not universally valid. Later, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
was able to prove that, to a large extent, the Dirichlet principle is valid under the hypothesis that Riemann was working with. However, in order to be valid, the Dirichlet principle needs certain hypotheses concerning the boundary of
which are not valid for simply connected domains in general. Simply connected domains with arbitrary boundaries were first treated by .The first proof of the theorem is due to Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
, who published it in 1912. His proof used Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s and it was simplified by Paul Koebe
Paul Koebe
Paul Koebe was a 20th-century German mathematician. His work dealt exclusively with the complex numbers, his most important results being on the uniformization of Riemann surfaces in a series of four papers in 1907–1909. He did his thesis at Berlin, where he worked under Herman Schwarz...
two years later in a way which did not require them.
Another proof, due to Leopold Fejér
Lipót Fejér
Lipót Fejér , was a Hungarian mathematician. Fejér was born Leopold Weiss, and changed to the Hungarian name Fejér around 1900....
and to Frigyes Riesz
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
, was published in 1922 and it was rather shorter than the previous ones. In this proof, like in Riemann's proof, the desired mapping was obtained as the solution of an extremal problem. The Fejér-Riesz proof was further simplified by Alexander Ostrowski and by Carathéodory.
Importance
The following points detail the uniqueness and power of the Riemann mapping theorem:- Even relatively simple Riemann mappings (for example a map from the interior of a circle to the interior of a square) have no explicit formula using only elementary functions.
- Simply connected open sets in the plane can be highly complicated, for instance the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
can be a nowhere-differentiable fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
curve of infinite length, even if the set itself is bounded. The fact that such a set can be mapped in an angle-preserving manner to the nice and regular unit disc seems counter-intuitive. - The analog of the Riemann mapping theorem for more complicated domains is not true. The next simplest case is of doubly connected domains (domains with a single hole). Any doubly connected domain except for the punctured disk and the punctured plane is conformally equivalent to some annulus {
: r < 
< 1 } with 0 < r < 1, however there are no conformal maps between annuliAnnulus (mathematics)In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
except inversion and multiplication by constants so the annulus {
: 1 < 
< 2 } is not conformally equivalent to the annulus { 
: 1 < 
< 4 } (as can be proven using extremal length). - The analogue of the Riemann mapping theorem in three or more real dimensions is not true. The family of conformal maps in three dimensions is very poor, and essentially contains only Möbius transformations.
- Even if arbitrary homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s in higher dimensions are permitted, contractible manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s can be found that are not homeomorphic to the ball (e.g. the Whitehead continuum). - The Riemann mapping theorem is the easiest way to prove that any two simply connected domains in the plane are homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. Even though the class of continuous functions is vastly larger than that of conformal maps, it is not easy to construct a one-to-one function onto the disk knowing only that the domain is simply connected.
A proof sketch
Given and , we want to construct a function which maps to the unit disk and to . For this sketch, we will assume that is bounded and its boundary is smooth, much like Riemann did. Writewhere
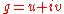is some (to be determined) holomorphic function with real part and imaginary part . It is then clear that z0 is the only zero of f. We require for on the boundary of , so we need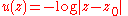on the boundary. Since
is the real part of a holomorphic function, we know that is necessarily a harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
, i.e. it satisfies Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
.
The question then becomes: does a real-valued harmonic function
exist that is defined on all of and has the given boundary condition? The positive answer is provided by the Dirichlet principle. Once the existence of u has been established, the Cauchy-Riemann equationsCauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
for the holomorphic function
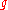allow us to find (this argument depends on the assumption that be simply connected). Once and have been constructed, one has to check that the resulting function does indeed have all the required properties.Uniformization theorem
The Riemann mapping theorem can be generalized to the context of Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s: If U is a simply-connected open subset of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, then U is biholomorphic to one of the following: the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
or the open unit disk. This is known as the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
.
See also
- Carathéodory's theoremCarathéodory's theorem (conformal mapping)In mathematical complex analysis, Carathéodory's theorem, proved by , states that if U is a simply connected open subset of the complex plane C, whose boundary is a Jordan curve Γ then the Riemann map...
- Measurable Riemann mapping theoremMeasurable Riemann mapping theoremIn the mathematical theory of quasiconformal mappings in two dimensions, the measurable Riemann mapping theorem, proved by , generalizes the Riemann mapping theorem from conformal to quasiconformal homeomorphisms, and is stated as follows...