Q-derivative
Encyclopedia
In mathematics
, in the area of combinatorics
, the q-derivative, or Jackson derivative, is a q-analog
of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration
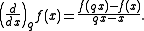
It is also often written as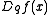
. The q-derivative is also known as the Jackson derivative. It is a linear operator
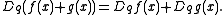
It has product rule analogous to the ordinary derivative product rule which has two equivalent forms
Similarly it satisfies a quotient rule
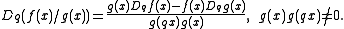
There is also a rule similar to the chain rule for ordinary derivatives. Let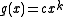
. Then
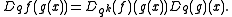
is:
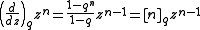
where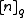
is the q-bracket of n. Note that 
so the ordinary derivative is regained in this limit.
The n-th q-derivative of a function may be given as:
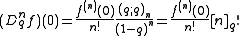
provided that the ordinary n-th derivative of f exists at x=0. Here,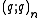
is the q-Pochhammer symbol, and 
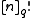is the q-factorial. If 
is analytic we can apply the Taylor formula to the definition of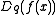 
to get
A q-analog of the Taylor expansion of a function about zero follows:
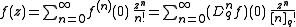
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the q-derivative, or Jackson derivative, is a q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration
Jackson integral
In q-analog theory, the Jackson integral series in the theory of special functions that expresses the operation inverse to q-differentiation.The Jackson integral was introduced by Frank Hilton Jackson.- Definition :...
Definition
The q-derivative of a function f(x) is defined as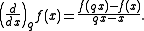It is also often written as
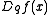. The q-derivative is also known as the Jackson derivative. It is a linear operator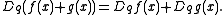It has product rule analogous to the ordinary derivative product rule which has two equivalent forms
Similarly it satisfies a quotient rule
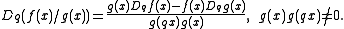
There is also a rule similar to the chain rule for ordinary derivatives. Let
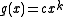. Then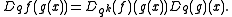Relationship to ordinary derivatives
Q-differentiation resembles ordinary differentiation, with curious differences. For example, the q-derivative of the monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
is:
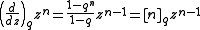
where
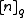is the q-bracket of n. Note that so the ordinary derivative is regained in this limit.The n-th q-derivative of a function may be given as:
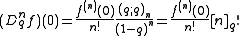
provided that the ordinary n-th derivative of f exists at x=0. Here,
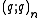is the q-Pochhammer symbol, and 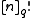is the q-factorial. If is analytic we can apply the Taylor formula to the definition of 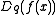to getA q-analog of the Taylor expansion of a function about zero follows:
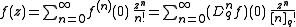
See also
- Derivative (generalizations)Derivative (generalizations)The derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, and geometry.- Derivatives in analysis :...
- Jackson integralJackson integralIn q-analog theory, the Jackson integral series in the theory of special functions that expresses the operation inverse to q-differentiation.The Jackson integral was introduced by Frank Hilton Jackson.- Definition :...
- Q-exponential
- Q-difference polynomialQ-difference polynomialIn combinatorial mathematics, the q-difference polynomials or q-harmonic polynomials are a polynomial sequence defined in terms of the q-derivative. They are a type of Brenke polynomial, and generalize the Appell polynomials...
s - Quantum calculusQuantum calculusQuantum calculus is equivalent to traditional infinitesimal calculus without the notion of limits. It defines "q-calculus" and "h-calculus". h ostensibly stands for Planck's constant while q stands for quantum...
- Tsallis entropyTsallis entropyIn physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
Further reading
- J. Koekoek, R. Koekoek, A note on the q-derivative operator, (1999) ArXiv math/9908140
- Thomas Ernst, The History of q-Calculus and a new method,(2001),