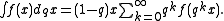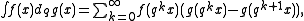Jackson integral
Encyclopedia
In q-analog
theory, the Jackson integral series
in the theory of special functions
that expresses the operation inverse to q-differentiation.
The Jackson integral was introduced by Frank Hilton Jackson.
More generally, if g(x) is another function and Dqg denotes its q-derivative, we can formally write
giving a q-analogue of the Riemann–Stieltjes integral.
of a continuous function
can be represented by its Riemann integral
, it is possible to show that the Jackson integral gives a unique q-antiderivative
within a certain class of functions.
If 
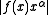is bounded on the interval 
for some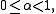 
then the Jackson integral converges to a functi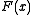on 
on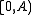 
which is a q-antiderivative of 
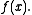Moreover, 
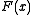is continuous at 
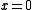with 
and is a unique antiderivative of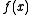 
in this class of functions.
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
theory, the Jackson integral series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
in the theory of special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
that expresses the operation inverse to q-differentiation.
The Jackson integral was introduced by Frank Hilton Jackson.
Definition
Let f(x) be a function of a real variable x. The Jackson integral of f is defined by the following series expansion:
More generally, if g(x) is another function and Dqg denotes its q-derivative, we can formally write
-
or
giving a q-analogue of the Riemann–Stieltjes integral.
Jackson integral as q-antiderivative
Just as the ordinary antiderivativeAntiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
can be represented by its Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, it is possible to show that the Jackson integral gives a unique q-antiderivative
within a certain class of functions.
Theorem
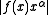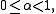Suppose that If is bounded on the interval for some then the Jackson integral converges to a functi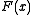on on 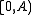which is a q-antiderivative of 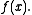Moreover, 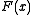is continuous at 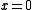with and is a unique antiderivative of 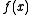in this class of functions.