Special functions
Encyclopedia
Special functions are particular mathematical function
s which have more or less established names and notations due to their importance in mathematical analysis
, functional analysis
, physics
, or other applications.
There is no general formal definition, but the list of mathematical functions contains functions which are commonly accepted as special.
In particular, elementary functions are also considered as special functions.
s
or integral
s of elementary functions. Therefore, tables of integrals
usually include descriptions of special functions, and tables of special functions
include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie group
s and Lie algebra
s, as well as certain topics in mathematical physics
.
Symbolic computation engines usually recognize the majority of special functions. Not all such systems have efficient algorithms for the evaluation, especially in the complex plane.
open parenthesis, then arguments, separated with comma, and then close parenthesis. Such a notation allows easy translation of the expressions to algorithmic languages avoiding ambiguities. Functions with established international notations are sin, cos, exp, erf
, and erfc.
Sometimes, a special function has several names.
The natural logarithm can be called as Log, log or ln, depending on the context.
For example, the tangent function may be denoted Tan, tan or tg (especially in Russian literature); arctangent may be called atan, arctg, or
. Bessel function
s may be written
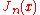; usually,
,
,
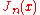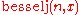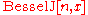refer to the same function.
Subscripts are often used to indicate arguments, typically integers.
In a few cases, the semicolon or even backslash (\) is used as a separator.
In this case, the translation to algorithmic languages admits ambiguity and may lead to confusion.
Superscripts may indicate not only exponentiation, but modification of a function. Examples include:
analytic
; the singularities and cuts are described; the differential and integral representations are known and the expansion to the Taylor or asymptotic series are available.
In addition, sometimes there exist relations with other special functions; a complicated special function can be expressed in terms of simpler functions. Various representations can be used for the evaluation; the simplest way to evaluate a function is to expand it into a Taylor series
.
However, such representation may converge slowly if at all. In algorithmic languages, rational approximations are typically used, although they may behave badly in the case of complex argument(s).
can be codified, as was clear already to expert mathematicians of the eighteenth century (if not before), the search for a complete and unified theory of special functions has continued since the nineteenth century. The high point of special function theory in the period 1850-1900 was the theory of elliptic function
s; treatises that were essentially complete, such as that of Tannery and Molk, could be written as handbooks to all the basic identities of the theory. They were based on techniques from complex analysis
.
From that time onwards it would be assumed that analytic function
theory, which had already unified the trigonometric and exponential function
s, was a fundamental tool. The end of the century also saw a very detailed discussion of spherical harmonic
s.
; applications to the physical sciences and engineering determined the relative importance of functions. In the days before the electronic computer, the ultimate compliment to a special function was the computation, by hand, of extended tables of its values
. This was a capital-intensive process, intended to make the function available by look-up, as for the familiar logarithm tables. The aspects of the theory that then mattered might then be two:
In contrast, one might say, there are approaches typical of the interests of pure mathematics
: asymptotic analysis
, analytic continuation
and monodromy
in the complex plane
, and the discovery of symmetry
principles and other structure behind the façade of endless formulae in rows. There is not a real conflict between these approaches, in fact.
(1902) textbook sought to unify the theory by using complex variables; the G. N. Watson
tome A Treatise on the Theory of Bessel Functions pushed the techniques as far as possible for one important type that particularly admitted asymptotics to be studied.
The later Bateman manuscript project
, under the editorship of Arthur Erdélyi
, attempted to be encyclopedic, and came around the time when electronic computation was coming to the fore and tabulation ceased to be the main issue.
is of a definite but limited scope. Hypergeometric series
became an intricate theory, in need of later conceptual arrangement. Lie group
s, and in particular their representation theory
, explain what a spherical function
can be in general; from 1950 onwards substantial parts of classical theory could be recast in terms of Lie groups. Further, work on algebraic combinatorics
also revived interest in older parts of the theory. Conjectures of Ian G. Macdonald
helped to open up large and active new fields with the typical special function flavour. Difference equations have begun to take their place besides differential equation
s as a source for special functions.
, certain special functions have traditionally been studied, such as particular Dirichlet series and modular form
s. Almost all aspects of special function theory are reflected there, as well as some new ones, such as came out of the monstrous moonshine
theory.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s which have more or less established names and notations due to their importance in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, or other applications.
There is no general formal definition, but the list of mathematical functions contains functions which are commonly accepted as special.
In particular, elementary functions are also considered as special functions.
Tables of special functions
Many special functions appear as solutions of differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s
or integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s of elementary functions. Therefore, tables of integrals
usually include descriptions of special functions, and tables of special functions
include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, as well as certain topics in mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
.
Symbolic computation engines usually recognize the majority of special functions. Not all such systems have efficient algorithms for the evaluation, especially in the complex plane.
Notations used in special functions
In most cases, the standard notation is used for indication of a special function: the name of function, subscripts, if any,open parenthesis, then arguments, separated with comma, and then close parenthesis. Such a notation allows easy translation of the expressions to algorithmic languages avoiding ambiguities. Functions with established international notations are sin, cos, exp, erf
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
, and erfc.
Sometimes, a special function has several names.
The natural logarithm can be called as Log, log or ln, depending on the context.
For example, the tangent function may be denoted Tan, tan or tg (especially in Russian literature); arctangent may be called atan, arctg, or
. Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s may be written
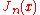; usually,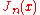,,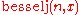 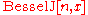refer to the same function.Subscripts are often used to indicate arguments, typically integers.
In a few cases, the semicolon or even backslash (\) is used as a separator.
In this case, the translation to algorithmic languages admits ambiguity and may lead to confusion.
Superscripts may indicate not only exponentiation, but modification of a function. Examples include:
-
usually indicates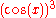 
-
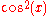is typically 
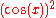, but never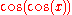 
-
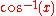usually means 
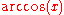, and not 
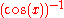; this one typically causes the most confusion, as it is inconsistent with the others.
Evaluation of special functions
Most special functions are considered as a function of a complex variable. They areanalytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
; the singularities and cuts are described; the differential and integral representations are known and the expansion to the Taylor or asymptotic series are available.
In addition, sometimes there exist relations with other special functions; a complicated special function can be expressed in terms of simpler functions. Various representations can be used for the evaluation; the simplest way to evaluate a function is to expand it into a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
.
However, such representation may converge slowly if at all. In algorithmic languages, rational approximations are typically used, although they may behave badly in the case of complex argument(s).
Classical theory
While trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
can be codified, as was clear already to expert mathematicians of the eighteenth century (if not before), the search for a complete and unified theory of special functions has continued since the nineteenth century. The high point of special function theory in the period 1850-1900 was the theory of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s; treatises that were essentially complete, such as that of Tannery and Molk, could be written as handbooks to all the basic identities of the theory. They were based on techniques from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.
From that time onwards it would be assumed that analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
theory, which had already unified the trigonometric and exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s, was a fundamental tool. The end of the century also saw a very detailed discussion of spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s.
Changing and fixed motivations
Of course the wish for a broad theory including as many as possible of the known special functions has its intellectual appeal, but it is worth noting other motivations. For a long time, the special functions were in the particular province of applied mathematicsApplied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
; applications to the physical sciences and engineering determined the relative importance of functions. In the days before the electronic computer, the ultimate compliment to a special function was the computation, by hand, of extended tables of its values
Mathematical table
Before calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
. This was a capital-intensive process, intended to make the function available by look-up, as for the familiar logarithm tables. The aspects of the theory that then mattered might then be two:
- for numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, discovery of infinite series or other analytical expressionAnalytical expressionIn mathematics, an analytical expression is a mathematical expression, constructed using well-known operations that lend themselves readily to calculation...
allowing rapid calculation; and - reduction of as many functions as possible to the given function.
In contrast, one might say, there are approaches typical of the interests of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
: asymptotic analysis
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
, analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
and monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, and the discovery of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
principles and other structure behind the façade of endless formulae in rows. There is not a real conflict between these approaches, in fact.
Twentieth century
The twentieth century saw several waves of interest in special function theory. The classic Whittaker and WatsonWhittaker and Watson
Whittaker and Watson is the informal name of a book formally titled A Course of Modern Analysis, written by E. T. Whittaker and G. N. Watson, first published by Cambridge University Press in 1902...
(1902) textbook sought to unify the theory by using complex variables; the G. N. Watson
G. N. Watson
Neville Watson was an English mathematician, a noted master in the application of complex analysis to the theory of special functions. His collaboration on the 1915 second edition of E. T. Whittaker's A Course of Modern Analysis produced the classic “Whittaker & Watson” text...
tome A Treatise on the Theory of Bessel Functions pushed the techniques as far as possible for one important type that particularly admitted asymptotics to be studied.
The later Bateman manuscript project
Bateman Manuscript Project
The Bateman Manuscript Project was a major effort at collation and encyclopedic compilation of the mathematical theory of special functions. It resulted in the eventual publication of five important reference volumes, under the editorship of Arthur Erdélyi....
, under the editorship of Arthur Erdélyi
Arthur Erdélyi
Arthur Erdélyi FRS, FRSE was a Hungarian-born British mathematician. Erdélyi was a leading expert on special functions - especially orthogonal polynomials and hypergeometric functions.-Biography:...
, attempted to be encyclopedic, and came around the time when electronic computation was coming to the fore and tabulation ceased to be the main issue.
Contemporary theories
The modern theory of orthogonal polynomialsOrthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
is of a definite but limited scope. Hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
became an intricate theory, in need of later conceptual arrangement. Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, and in particular their representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, explain what a spherical function
Spherical function
Spherical function can refer to* Spherical harmonics*Zonal spherical function...
can be in general; from 1950 onwards substantial parts of classical theory could be recast in terms of Lie groups. Further, work on algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
also revived interest in older parts of the theory. Conjectures of Ian G. Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
helped to open up large and active new fields with the typical special function flavour. Difference equations have begun to take their place besides differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s as a source for special functions.
Special functions in number theory
In number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, certain special functions have traditionally been studied, such as particular Dirichlet series and modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. Almost all aspects of special function theory are reflected there, as well as some new ones, such as came out of the monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
theory.
External links
- Special functions, Special functions calculator.
- Online calculator, Online scientific calculator with over 100 functions (>=32 digits, many complex)
- Special functions at EqWorld: The World of Mathematical Equations.
- Special functions and polynomials'' by 't Hooft and Nobbenhuis
- NIST Digital Library of Mathematical Functions, Frank W. J. Olver, Daniel W. Lozier, Ronald F. Boisvert, and Charles W. Clark (Editors) (2010).
- Numerical Methods for Special Functions, by A. Gil, J. Segura, N.M. Temme (2007).
- R. Jagannathan, (P,Q)-Special Functions