Monodromy
Encyclopedia
In mathematics
, monodromy is the study of how objects from mathematical analysis
, algebraic topology
and algebraic
and differential geometry behave as they 'run round' a singularity
. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'. It is closely associated with covering map
s and their degeneration into ramification
; the aspect giving rise to monodromy phenomena is that certain function
s we may wish to define fail to be single-valued as we 'run round' a path encircling a singularity. The failure of monodromy is best measured by defining a monodromy group: a group
of transformations acting on the data that encodes what does happen as we 'run round'.
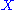be a connected and locally connected based topological space
with base point x, and let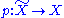
be a covering
with fiber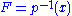
. For a loop 
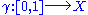based at 
, denote a lift
under the covering map (starting at a point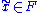
) by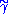 
. Finally, we denote by 
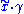the endpoint 
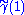, which is generally different from 
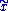. There are theorems which state that this construction gives a well-defined group action
of the fundamental group
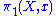on F, and that the stabilizer of 
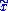is exactly 
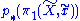, that is, an element 
fixes a point in F if and only if it is represented by the image of a loop in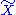 
based at 
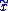. This action is called the monodromy action and the corresponding homomorphism
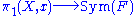into the symmetric group
on F is the monodromy. The image of this homomorphism is the monodromy group.
. In the process of analytic continuation
, a function that is an analytic function
F(z) in some open subset E of the punctured disk D ={z ∈ C: 0 < |z| < 1} may be continued back into E, but with different values. For example take
then analytic continuation anti-clockwise round the circle
will result in the return, not to F(z) but
In this case the monodromy group is infinite cyclic and the covering space is the universal cover of the punctured complex plane. This cover can be visualized as the helicoid
(as defined in the helicoid article) restricted to
. The covering map is a vertical projection, in a sense collapsing the spiral in the obvious way to get a punctured plane.
s, where a single solution may give further linearly independent solutions by analytic continuation
. Linear differential equations defined in an open, connected set S in the complex plane have a monodromy group, which (more precisely) is a linear representation of the fundamental group
of S, summarising all the analytic continuations round loops within S. The inverse problem, of constructing the equation (with regular singularities), given a representation, is called the Riemann–Hilbert problem.
, and use the homotopy lifting property
to 'follow' paths on the base space X (we assume it path-connected for simplicity) as they are lifted up into the cover C. If we follow round a loop based at x in X, which we lift to start at c above x, we'll end at some c* again above x; it is quite possible that c ≠ c*, and to code this one considers the action of the fundamental group
π1(X,x) as a permutation group
on the set of all c, as a monodromy group in this context.
In differential geometry, an analogous role is played by parallel transport
. In a principal bundle
B over a smooth manifold M, a connection
allows 'horizontal' movement from fibers above m in M to adjacent ones. The effect when applied to loops based at m is to define a holonomy
group of translations of the fiber at m; if the structure group of B is G, it is a subgroup of G that measures the deviation of B from the product bundle MxG.
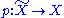. The result has the structure of a groupoid
over the base space X. The advantage is that we can drop the condition of connectedness of X.
Moreover the construction can also be generalized to foliation
s: Consider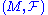
a (possibly singular) foliation of M. Then for every path in a leaf of 
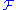we can consider its induced diffeomorphism on local transversal sections through the endpoints. Within a simply connected chart this diffeomorphism becomes unique and especially canonical between different transversal sections if we go over to the germ
of the diffeomorphism around the endpoints. In this way it also becomes independent of the path (between fixed endpoints) within a simply connected chart and is therefore invariant under homotopy.
of the ring
F[x] where F is also a field
. An element f(y) ∈ F(y) determines a finite field extension
[F(x) : F(y)] by setting
This extension is generally not Galois but which has Galois closure L(f). The associated Galois group
of the extension [L(f) : F(x)] is called the monodromy group of the extension.
In the case of F = C Riemann surface
theory enters and allows for the geometric interpretation given above. In the case that the extension C(y) is already Galois, the associated monodromy group is sometimes called a group of deck transformations
.
This has connections with the Galois theory of covering spaces
leading to the Riemann existence theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, monodromy is the study of how objects from mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and algebraic
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and differential geometry behave as they 'run round' a singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'. It is closely associated with covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
s and their degeneration into ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
; the aspect giving rise to monodromy phenomena is that certain function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s we may wish to define fail to be single-valued as we 'run round' a path encircling a singularity. The failure of monodromy is best measured by defining a monodromy group: a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of transformations acting on the data that encodes what does happen as we 'run round'.
Definition
Let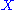 be a connected and locally connected based topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with base point x, and let
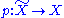be a coveringCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
with fiber
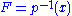. For a loop 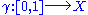based at , denote a liftHomotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
under the covering map (starting at a point
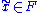) by 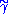. Finally, we denote by 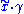the endpoint 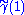, which is generally different from 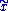. There are theorems which state that this construction gives a well-defined group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
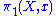on F, and that the stabilizer of 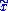is exactly 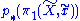, that is, an element fixes a point in F if and only if it is represented by the image of a loop in 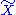based at 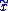. This action is called the monodromy action and the corresponding homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
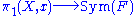into the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on F is the monodromy. The image of this homomorphism is the monodromy group.
Example
These ideas were first made explicit in complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. In the process of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
, a function that is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
F(z) in some open subset E of the punctured disk D ={z ∈ C: 0 < |z| < 1} may be continued back into E, but with different values. For example take
-
- F(z) = log z
- E = {z ∈ C: Re(z) > 0}
then analytic continuation anti-clockwise round the circle
-
- |z| = 0.5
will result in the return, not to F(z) but
-
- F(z)+2πi.
In this case the monodromy group is infinite cyclic and the covering space is the universal cover of the punctured complex plane. This cover can be visualized as the helicoid
Helicoid
The helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
(as defined in the helicoid article) restricted to
. The covering map is a vertical projection, in a sense collapsing the spiral in the obvious way to get a punctured plane.Differential equations in the complex domain
One important application is to differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, where a single solution may give further linearly independent solutions by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. Linear differential equations defined in an open, connected set S in the complex plane have a monodromy group, which (more precisely) is a linear representation of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of S, summarising all the analytic continuations round loops within S. The inverse problem, of constructing the equation (with regular singularities), given a representation, is called the Riemann–Hilbert problem.
Topological and geometric aspects
In the case of a covering map, we look at it as a special case of a fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
, and use the homotopy lifting property
Homotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
to 'follow' paths on the base space X (we assume it path-connected for simplicity) as they are lifted up into the cover C. If we follow round a loop based at x in X, which we lift to start at c above x, we'll end at some c* again above x; it is quite possible that c ≠ c*, and to code this one considers the action of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π1(X,x) as a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
on the set of all c, as a monodromy group in this context.
In differential geometry, an analogous role is played by parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
. In a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
B over a smooth manifold M, a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
allows 'horizontal' movement from fibers above m in M to adjacent ones. The effect when applied to loops based at m is to define a holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
group of translations of the fiber at m; if the structure group of B is G, it is a subgroup of G that measures the deviation of B from the product bundle MxG.
Monodromy groupoid and Foliations
Analogous to the Fundamental groupoid it is possible to get rid of the choice of a base point and to define a monodromy groupoid. Here we consider (homotopy classes of) lifts of paths in the base space X of a fibration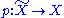. The result has the structure of a groupoidGroupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
over the base space X. The advantage is that we can drop the condition of connectedness of X.
Moreover the construction can also be generalized to foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s: Consider
a (possibly singular) foliation of M. Then for every path in a leaf of we can consider its induced diffeomorphism on local transversal sections through the endpoints. Within a simply connected chart this diffeomorphism becomes unique and especially canonical between different transversal sections if we go over to the germGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of the diffeomorphism around the endpoints. In this way it also becomes independent of the path (between fixed endpoints) within a simply connected chart and is therefore invariant under homotopy.
Definition via Galois theory
Let F(x) denote the field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
F[x] where F is also a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. An element f(y) ∈ F(y) determines a finite field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
[F(x) : F(y)] by setting
-
- f(y) = x.
This extension is generally not Galois but which has Galois closure L(f). The associated Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the extension [L(f) : F(x)] is called the monodromy group of the extension.
In the case of F = C Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory enters and allows for the geometric interpretation given above. In the case that the extension C(y) is already Galois, the associated monodromy group is sometimes called a group of deck transformations
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
.
This has connections with the Galois theory of covering spaces
Grothendieck's Galois theory
In mathematics, Grothendieck's Galois theory is a highly abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry...
leading to the Riemann existence theorem.
See also
- Braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
- Monodromy theoremMonodromy theoremIn complex analysis, the monodromy theorem is an important result about analytic continuation of a complex-analytic function to a larger set. The idea is that one can extend a complex-analytic function along curves starting in the original domain of the function and ending in the larger set...
- Mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
(of a punctured disk)