Homotopy lifting property
Encyclopedia
In mathematics
, in particular in homotopy theory within algebraic topology
, the homotopy lifting property (also known as the right lifting property or the covering homotopy axiom) is a technical condition on a continuous function
from a topological space
E to another one, B. It is designed to support the picture of E 'above' B, by allowing a homotopy
taking place in B to be moved 'upstairs' to E. For example, a covering map
has a property of unique local lifting of paths to a given sheet; the uniqueness is to do with the fact that the fibers of a covering map are discrete space
s. The homotopy lifting property will hold in many situations, such as the projection in a vector bundle
, fiber bundle
or fibration
, where there need be no unique way of lifting.
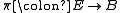, and a space X, one says that (X,π) has the homotopy lifting property, or that π has the homotopy lifting property with respect to X, if:
there exists a homotopy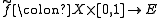
lifting 
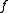(i.e. so that 
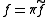) with 
.
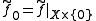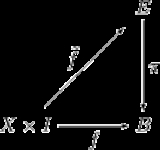
The following diagram visualizes this situation.
The outer square (without the dotted arrow) commutes if and only if the hypotheses of the lifting property are true. A lifting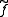
corresponds to a dotted arrow making the diagram commute. Also compare this to the visualization of the homotopy extension property.
If the map
satisfies the homotopy lifting property with respect to all spaces X, then 
is called a fibration
, or one sometimes simply says that
has the homotopy lifting property.
N.B. This is the definition of fibration in the sense of Hurewicz, which is more restrictive than fibration in the sense of Serre
, for which homotopy lifting only for X a CW complex
is required.
. Given a pair of spaces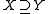
, for simplicity we denote 
. Given additionally a map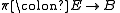 
, one says that 
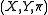has the homotopy lifting extension property if:
there exists a homotopy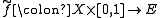
which extends 
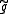(i.e. such that 
).
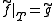The homotopy lifting property of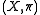
is obtained by taking Y = ø, so that T above is simply 
.
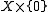The homotopy extension property of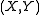
is obtained by taking 
to be a constant map, so that π is irrelevant in that every map to E is trivially the lift of a constant map to the image point of π).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in homotopy theory within algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the homotopy lifting property (also known as the right lifting property or the covering homotopy axiom) is a technical condition on a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
from a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
E to another one, B. It is designed to support the picture of E 'above' B, by allowing a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
taking place in B to be moved 'upstairs' to E. For example, a covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
has a property of unique local lifting of paths to a given sheet; the uniqueness is to do with the fact that the fibers of a covering map are discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
s. The homotopy lifting property will hold in many situations, such as the projection in a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
or fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
, where there need be no unique way of lifting.
Formal definition
Assume from now on all mappings are continuous functions from a topological space to another. Given a map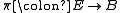, and a space X, one says that (X,π) has the homotopy lifting property, or that π has the homotopy lifting property with respect to X, if:- for any homotopyHomotopyIn topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
, and - for any map
lifting 
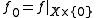(i.e. so that 
),
there exists a homotopy
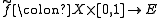lifting 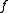(i.e. so that 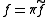) with 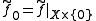.The following diagram visualizes this situation.
The outer square (without the dotted arrow) commutes if and only if the hypotheses of the lifting property are true. A lifting
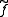corresponds to a dotted arrow making the diagram commute. Also compare this to the visualization of the homotopy extension property.If the map
satisfies the homotopy lifting property with respect to all spaces X, then is called a fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
, or one sometimes simply says that
has the homotopy lifting property.N.B. This is the definition of fibration in the sense of Hurewicz, which is more restrictive than fibration in the sense of Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, for which homotopy lifting only for X a CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is required.
Generalization: The Homotopy Lifting Extension Property
There is a common generalization of the homotopy lifting property and the homotopy extension propertyHomotopy extension property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates when a homotopy defined on a subspace can be extended to a homotopy defined on a larger space.-Definition:Let X\,\! be a topological space, and let A \subset X....
. Given a pair of spaces
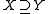, for simplicity we denote . Given additionally a map 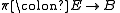, one says that 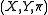has the homotopy lifting extension property if:- for any homotopyHomotopyIn topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
, and - for any lifting
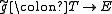of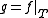 
,
there exists a homotopy
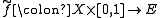which extends 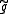(i.e. such that 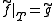).The homotopy lifting property of
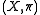is obtained by taking Y = ø, so that T above is simply 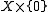.The homotopy extension property of
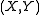is obtained by taking to be a constant map, so that π is irrelevant in that every map to E is trivially the lift of a constant map to the image point of π).