
Homotopy extension property
Encyclopedia
In mathematics
, in the area of algebraic topology
, the homotopy extension property indicates when a homotopy
defined on a subspace
can be extended to a homotopy defined on a larger space.
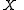 be a topological space
be a topological space
, and let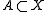 .
.
Given a homotopy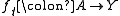 and a map
and a map 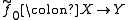 such that
such that 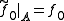 ,
,
we say that the pair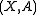 has the homotopy extension property if
has the homotopy extension property if
there exists an extension of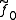 to the homotopy
to the homotopy 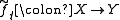 such that
such that
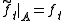 .
.
That is, the pair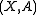 has the homotopy extension property if any map
has the homotopy extension property if any map
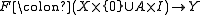
can be extended to a map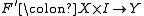 (i.e.
(i.e.  and
and 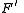 agree on their common domain).
agree on their common domain).
If the pair has this property only for a certain codomain
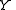 , we say that
, we say that 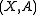 has the homotopy extension property with respect to
has the homotopy extension property with respect to 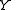 .
.
 If the above diagram (without the dashed map) commutes, which is equivalent to the conditions above, then there exists a map
If the above diagram (without the dashed map) commutes, which is equivalent to the conditions above, then there exists a map 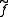 which makes the diagram commute. By currying
which makes the diagram commute. By currying
, note that a map is the same as a map
is the same as a map 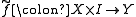 .
.
Also compare this to the visualization of the homotopy lifting property.
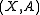 has the homotopy extension property, then the simple inclusion map
has the homotopy extension property, then the simple inclusion map 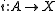 is a cofibration
is a cofibration
.
In fact, if you consider any cofibration
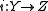 , then we have that
, then we have that 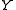 is homeomorphic to its image under
is homeomorphic to its image under 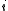 . This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.
. This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the homotopy extension property indicates when a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
defined on a subspace
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
can be extended to a homotopy defined on a larger space.
Definition
Let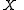 be a topological space
be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and let
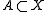 .
.Given a homotopy
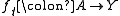 and a map
and a map 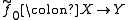 such that
such that 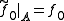 ,
,we say that the pair
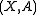 has the homotopy extension property if
has the homotopy extension property ifthere exists an extension of
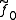 to the homotopy
to the homotopy 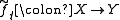 such that
such that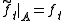 .
. That is, the pair
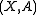 has the homotopy extension property if any map
has the homotopy extension property if any map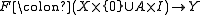
can be extended to a map
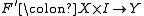 (i.e.
(i.e.  and
and 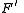 agree on their common domain).
agree on their common domain).If the pair has this property only for a certain codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
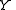 , we say that
, we say that 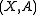 has the homotopy extension property with respect to
has the homotopy extension property with respect to 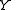 .
.Visualisation
The homotopy extension property is depicted in the following diagram
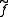 which makes the diagram commute. By currying
which makes the diagram commute. By curryingCurrying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
, note that a map
 is the same as a map
is the same as a map 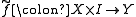 .
.Also compare this to the visualization of the homotopy lifting property.
Properties
- If
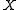 is a cell complex and
is a cell complex and 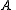 is a subcomplex of
is a subcomplex of  , then the pair
, then the pair 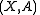 has the homotopy extension property.
has the homotopy extension property.
- A pair
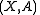 has the homotopy extension property if and only if
has the homotopy extension property if and only if 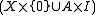 is a retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
is a retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of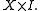
Other
If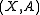 has the homotopy extension property, then the simple inclusion map
has the homotopy extension property, then the simple inclusion map 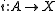 is a cofibration
is a cofibrationCofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
.
In fact, if you consider any cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
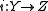 , then we have that
, then we have that 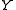 is homeomorphic to its image under
is homeomorphic to its image under 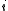 . This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.
. This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.

