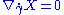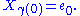Home Discussion Topics Dictionary Almanac

Signup Login

Parallel transport

Discussion

Ask a question about 'Parallel transport'

Start a new discussion about 'Parallel transport'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, parallel transport is a way of transporting geometrical data along smooth curves in a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

. If the manifold is equipped with an affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

(a covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

or connection

Connection (vector bundle)

In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...

on the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

), then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection. Other notions of connection

Connection (mathematics)

In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...

come equipped with their own parallel transportation systems as well. For instance, a Koszul connection in a vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

also allows for the parallel transport of vectors in much the same way as with a covariant derivative. An Ehresmann

Ehresmann connection

In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...

or Cartan connection

Cartan connection

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...

supplies a lifting of curves from the manifold to the total space of a principal bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

. Such curve lifting may sometimes be thought of as the parallel transport of reference frame

Reference frame

Reference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...

s.

The parallel transport for a connection thus supplies a way of, in some sense, moving the local geometry of a manifold along a curve: that is, of connecting the geometries of nearby points. There may be many notions of parallel transport available, but a specification of one — one way of connecting up the geometries of points on a curve — is tantamount to providing a connection. In fact, the usual notion of connection is the infinitesimal

Infinitesimal

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

analog of parallel transport. Or, vice versa, parallel transport is the local realization of a connection.

As parallel transport supplies a local realization of the connection, it also supplies a local realization of the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

known as holonomy

Holonomy

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...

. The Ambrose-Singer theorem makes explicit this relationship between curvature and holonomy.

Parallel transport on a vector bundle

Let M be a smooth manifold. Let E→M be a vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

with covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

∇ and γ: I→M a smooth curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

parameterized by an open interval I. A section

Section (fiber bundle)

In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...

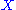of

along γ is called parallel if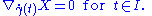

Suppose we are given an element e₀ ∈ E_P at P = γ(0) ∈ M, rather than a section. The parallel transport of e₀ along γ is the extension of e₀ to a parallel section X on γ.
More precisely, X is the unique section of E along γ such that

Note that in a local trivialization (1) defines an ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

, with the initial condition given by (2). Thus the Picard–Lindelöf theorem

Picard–Lindelöf theorem

In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...

guarantees the existence and uniqueness of the solution.

Thus the connection ∇ defines a way of moving elements of the fibers along a curve, and this provides linear isomorphisms between the fibers at points along the curve:

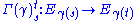
from the vector space lying over γ(s) to that over γ(t). This isomorphism is known as the parallel transport map associated to the curve. The isomorphisms between fibers obtained in this way will in general depend on the choice of the curve: if they do not then parallel transport along every curve can be used to define parallel sections of E over all of M. This is only possible if the curvature
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...

of ∇ is zero.

In particular, parallel transport around a closed curve starting at a point x defines an automorphism

Automorphism

In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...

of the tangent space at x which is not necessarily trivial. The parallel transport automorphisms defined by all closed curves based at x form a transformation group called the holonomy group of ∇ at x. There is a close relation between this group and the value of the curvature of ∇ at x; this is the content of the Ambrose-Singer holonomy theorem.

Recovering the connection from the parallel transport

Given a covariant derivative ∇, the parallel transport along a curve γ is obtained by integrating the condition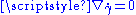

. Conversely, if a suitable notion of parallel transport is available, then a corresponding connection can be obtained by differentiation. This approach is due, essentially, to ; see . also adopts this approach.

Consider an assignment to each curve γ in the manifold a collection of mappings

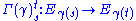
such that

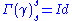, the identity transformation of E_γ(s).
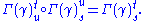
The dependence of Γ on γ, s, and t is "smooth."

The notion of smoothness in condition 3. is somewhat difficult to pin down (see the discussion below of parallel transport in fibre bundles). In particular, modern authors such as Kobayashi and Nomizu generally view the parallel transport of the connection as coming from a connection in some other sense, where smoothness is more easily expressed.

Nevertheless, given such a rule for parallel transport, it is possible to recover the associated infinitesimal connection in E as follows. Let γ be a differentiable curve in M with initial point γ(0) and initial tangent vector X = γ′(0). If V is a section of E over γ, then let

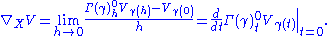
This defines the associated infinitesimal connection ∇ on E. One recovers the same parallel transport Γ from this infinitesimal connection.

Special case: The tangent bundle

Let M be a smooth manifold. Then a connection on the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

of M, called an affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

, distinguishes a class of curves called (affine) geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s . A smooth curve γ: I → M is an affine geodesic if

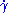is parallel transported along

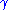, that is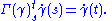

Taking the derivative with respect to time, this takes the more familiar form

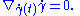
Parallel transport in Riemannian geometry

In (pseudo

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

) Riemannian geometry

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

, a metric connection

Metric connection

In mathematics, a metric connection is a connection in a vector bundle E equipped with a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve...

is any connection whose parallel transport mappings preserve the metric tensor

Metric tensor

In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...

. Thus a metric connection is any connection Γ such that, for any two vectors X, Y ∈ T_γ(s)

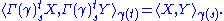
Taking the derivative at t=0, the associated differential operator ∇ must satisfy a product rule with respect to the metric:

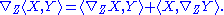
Geodesics

If ∇ is a metric connection, then the affine geodesic are the usual geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s of Riemannian geometry and are the locally distance minimizing curves. More precisely, first note that if γ: I → M, where I is an open interval, is a geodesic, then the norm of

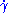is constant on I. Indeed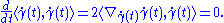

It follows from an application of Gauß's Lemma

Gauss's lemma (Riemannian geometry)

In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M...

that if A is the norm of

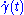then the distance, induced by the metric, between two close enough points on the curve γ, say γ(t₁) and γ(t₂), is given by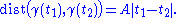

The formula above might not be true for points which are not close enough since the geodesic might for example wrap around the manifold (e.g. on a sphere).

Generalizations

The parallel transport can be defined in greater generality for other types of connections, not just those defined in a vector bundle. One generalization is for principal connections

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...

. Let P → M be a principal bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

over a manifold M with structure Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

G and a principal connection ω. As in the case of vector bundles, a principal connection ω on P defines, for each curve γ in M, a mapping

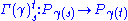
from the fibre over γ(s) to that over γ(t), which is an isomorphism of homogeneous space

Homogeneous space

In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...

s: i.e.

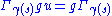for each g∈G.

Further generalizations of parallel transport are also possible. In the context of Ehresmann connection

Ehresmann connection

In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...

s, where the connection depends on a special notion of "horizontal lifting" of tangent spaces, one can define parallel transport via horizontal lifts. Cartan connection

Cartan connection

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...

s are Ehresmann connections with additional structure which allows the parallel transport to be though of as a map "rolling" a certain model space

Klein geometry

In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry.For background and motivation...

along a curve in the manifold. This rolling is called development

Development (differential geometry)

In classical differential geometry, development refers to the simple idea of rolling one smooth surface over another in Euclidean space. For example, the tangent plane to a surface at a point can be rolled around the surface to obtain the tangent-plane at other points.The tangential contact...

.

Approximation: Schild's ladder

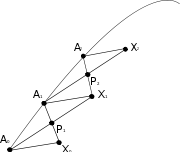
Parallel transport can be discretely approximated by Schild's ladder

Schild's ladder

In the theory of general relativity, and differential geometry more generally, Schild's ladder is a first-order method for approximating parallel transport of a vector along a curve using only affinely parametrized geodesics...

,
which takes finite steps along a curve, and approximates
Levi-Civita parallelogramoid

Levi-Civita parallelogramoid

In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space. It is named for its discoverer, Tullio Levi-Civita...

s by approximate parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

s.

External links

Spherical Geometry Demo. An applet demonstrating parallel transport of tangent vectors on a sphere.