Metric connection
Encyclopedia
In mathematics
, a metric connection is a connection
in a vector bundle
E equipped with a metric
for which the inner product of any two vectors will remain the same when those vectors are parallel transport
ed along any curve. Other common equivalent formulations of a metric connection include:
A special case of a metric connection is the Levi-Civita connection
. Here the bundle E is the tangent bundle
of a manifold. In addition to being a metric connection, the Levi-Civita connection is required to be torsion free
.
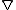on the tangent bundle
of a pseudo-Riemannian manifold
(M, g) such that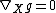
for all vector fields X on M. Equivalently, 
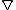is Riemannian if the parallel transport
it defines preserves the metric g.
A given connection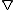
is Riemannian if and only if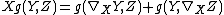
for all vector fields X, Y and Z on M, where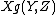
denotes the derivative of the function 
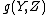along this vector field 
.
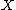The Levi-Civita connection
is the torsion-free
Riemannian connection on a manifold. It is unique by the fundamental theorem of Riemannian geometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a metric connection is a connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
in a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
E equipped with a metric
Metric (vector bundle)
In differential geometry, the notion of a metric tensor can be extended to an arbitrary vector bundle. Specifically, if M is a topological manifold and E → M a vector bundle on M, then a metric on E is a bundle map g : E ×M E → M × R from the fiber product of E with itself...
for which the inner product of any two vectors will remain the same when those vectors are parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
ed along any curve. Other common equivalent formulations of a metric connection include:
- A connection for which the covariant derivativeConnection (vector bundle)In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
s of the metric on E vanish. - A principal connectionConnection (principal bundle)In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
on the bundle of orthonormal frameOrthonormal frameIn Riemannian geometry and relativity theory, an orthonormal frame is a tool for studying the structure of a differentiable manifold equipped with a metric...
s of E.
A special case of a metric connection is the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
. Here the bundle E is the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a manifold. In addition to being a metric connection, the Levi-Civita connection is required to be torsion free
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
.
Riemannian connections
An important special case of a metric connection is a Riemannian connection. This is a connection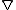 on the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
(M, g) such that
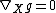for all vector fields X on M. Equivalently, 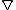is Riemannian if the parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
it defines preserves the metric g.
A given connection
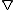is Riemannian if and only if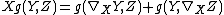for all vector fields X, Y and Z on M, where
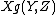denotes the derivative of the function 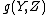along this vector field 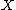.The Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
is the torsion-free
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
Riemannian connection on a manifold. It is unique by the fundamental theorem of Riemannian geometry
Fundamental theorem of Riemannian geometry
In Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold there is a unique torsion-free metric connection, called the Levi-Civita connection of the given metric...
.