Connection (principal bundle)
Encyclopedia
In mathematics
, a connection is a device that defines a notion of parallel transport
on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle
P over a smooth manifold M is a particular type of connection which is compatible with the action
of the group G.
A principal connection can be viewed as a special case of the notion of an Ehresmann connection
, and is sometimes called a principal Ehresmann connection. It gives rise to (Ehresmann) connections on any fiber bundle
associated to P via the associated bundle
construction. In particular, on any associated vector bundle the principal connection induces a covariant derivative
, an operator that can differentiate sections
of that bundle along tangent directions
in the base manifold. Principal connections generalize to arbitrary principal bundles the concept of a linear connection
on the frame bundle
of a smooth manifold.
over a smooth manifold M. Then a principal G-connection on P is a differential 1-form on P with values in the Lie algebra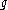
of G which is G-equivariant and reproduces the Lie algebra generators of the fundamental vector fields on P.
In other words, it is an element ω of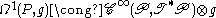
such that
Sometimes the term principal G-connection refers to the pair (P,ω) and ω itself is called the connection form
or connection 1-form of the principal connection.
on P in the following way. First note that the fundamental vector fields generating the G action on P provide a bundle isomorphism from the vertical bundle
V of P (with Vp=Tp(Pπ(p)) to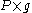
. It follows that ω determines uniquely a bundle map v:TP→V which is the identity on V. Such a projection v is uniquely determined by its kernel, which is a smooth subbundle H of TP (called the horizontal bundle
) such that TP=V⊕H. This is an Ehresmann connection.
Conversely, an Ehresmann connection H⊂TP (or v:TP→V) on P defines a principal G-connection ω if and only if it is G-equivariant in the sense that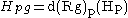
.
.
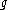If the section s is replaced by a new section sg, defined by (sg)(x) = s(x)g(x), where g:M→G is a smooth map, then (sg)*ω = Ad(g)-1 s*ω+g-1dg. The principal connection is uniquely determined by this family of
-valued 1-forms, and these 1-forms are also called connection forms or connection 1-forms, particularly in older or more physics-oriented literature.
TP by right translation. The quotient space
TP/G is also a manifold, and inherits the structure of a fibre bundle over TM which shall be denoted dπ:TP/G→TM. Let ρ:TP/G→M be the projection onto M. The fibres of the bundle TP/G under the projection ρ carry an additive structure.
The bundle TP/G is called the bundle of principal connections . A section
Γ of dπ:TP/G→TM such that Γ : TM → TP/G is a linear morphism of vector bundles over M, can be identified with a principal connection in P. Conversely, a principal connection as defined above gives rise to such a section Γ of TP/G.
Finally, let Γ be a principal connection in this sense. Let q:TP→TP/G be the quotient map. The horizontal distribution of the connection is the bundle
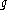-valued 1-form on P which is not only G-equivariant, but horizontal in the sense that it vanishes on any section of the vertical bundle V of P. Hence it is basic and so is determined by a 1-form on M with values in the adjoint bundle
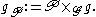
Conversely, any such one form defines (via pullback) a G-equivariant horizontal 1-form on P, and the space of principal G-connections is an affine space
for this space of 1-forms.
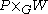over M, and a principal connection induces a covariant derivative
on any such vector bundle. This covariant derivative can be defined using the fact that the space of sections of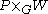
over M is isomorphic to the space of G-equivariant W-valued functions on P. More generally, the space of k-forms with values in 
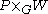is identified with the space of G-equivariant and horizontal W-valued k-forms on P. If α is such a k-form, then its exterior derivative
dα, although G-equivariant, is no longer horizontal. However, the combination dα+ωΛα is. This defines an exterior covariant derivative
dω from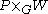
-valued k-forms on M to 
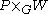-valued (k+1)-forms on M. In particular, when k=0, we obtain a covariant derivative on 
.
of a principal G-connection ω is the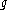
-valued 2-form Ω defined by
It is G-equivariant and horizontal, hence corresponds to a 2-form on M with values in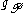
. The identification of the curvature with this quantity is sometimes called the second structure equation.
, or (more generally) if it has a solder form
, then the connection is an example of an affine connection
, and the curvature is not the only invariant, since the additional structure of the solder form θ, which is an equivariant Rn-valued 1-form on P, should be taken into account. In particular, the torsion form on P, is an Rn-valued 2-form Θ defined by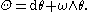
Θ is G-equivariant and horizontal, and so it descends to a tangent-valued 2-form on M, called the torsion. This equation is sometimes called the first structure equation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a connection is a device that defines a notion of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
P over a smooth manifold M is a particular type of connection which is compatible with the action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the group G.
A principal connection can be viewed as a special case of the notion of an Ehresmann connection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
, and is sometimes called a principal Ehresmann connection. It gives rise to (Ehresmann) connections on any fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
associated to P via the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
construction. In particular, on any associated vector bundle the principal connection induces a covariant derivative
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
, an operator that can differentiate sections
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of that bundle along tangent directions
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
in the base manifold. Principal connections generalize to arbitrary principal bundles the concept of a linear connection
Linear connection
In the mathematical field of differential geometry, the term linear connection can refer to either of the following overlapping concepts:* a connection on a vector bundle, often viewed as a differential operator ;* a principal connection on the frame bundle of a manifold or the induced connection...
on the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of a smooth manifold.
Formal Definition
Let π:P→M be a smooth principal G-bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over a smooth manifold M. Then a principal G-connection on P is a differential 1-form on P with values in the Lie algebra
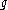of G which is G-equivariant and reproduces the Lie algebra generators of the fundamental vector fields on P.In other words, it is an element ω of
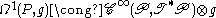such that
-
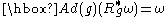where Rg denotes right multiplication by g; - if
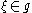and Xξ is the vector field on P associated to ξ by differentiating the G action on P, then ω(Xξ) = ξ (identically on P).
Sometimes the term principal G-connection refers to the pair (P,ω) and ω itself is called the connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
or connection 1-form of the principal connection.
Relation to Ehresmann connections
A principal G-connection ω on P determines an Ehresmann connectionEhresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
on P in the following way. First note that the fundamental vector fields generating the G action on P provide a bundle isomorphism from the vertical bundle
Vertical bundle
The vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
V of P (with Vp=Tp(Pπ(p)) to
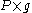. It follows that ω determines uniquely a bundle map v:TP→V which is the identity on V. Such a projection v is uniquely determined by its kernel, which is a smooth subbundle H of TP (called the horizontal bundleHorizontal bundle
In mathematics, in the field of differential topology, givena smooth fiber bundle over a smooth manifold M, then the vertical bundle VE of E is the subbundle of the tangent bundle TE consisting of the vectors which are tangent to the fibers of E over M...
) such that TP=V⊕H. This is an Ehresmann connection.
Conversely, an Ehresmann connection H⊂TP (or v:TP→V) on P defines a principal G-connection ω if and only if it is G-equivariant in the sense that
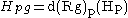.Form in a local trivialization
A local trivialization of a principal bundle P is given by a section s of P over an open subset U of M. Then the pullback s*ω of a principal connection is a 1-form on U with values in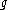.If the section s is replaced by a new section sg, defined by (sg)(x) = s(x)g(x), where g:M→G is a smooth map, then (sg)*ω = Ad(g)-1 s*ω+g-1dg. The principal connection is uniquely determined by this family of
-valued 1-forms, and these 1-forms are also called connection forms or connection 1-forms, particularly in older or more physics-oriented literature.Bundle of principal connections
The group G acts on the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TP by right translation. The quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
TP/G is also a manifold, and inherits the structure of a fibre bundle over TM which shall be denoted dπ:TP/G→TM. Let ρ:TP/G→M be the projection onto M. The fibres of the bundle TP/G under the projection ρ carry an additive structure.
The bundle TP/G is called the bundle of principal connections . A section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
Γ of dπ:TP/G→TM such that Γ : TM → TP/G is a linear morphism of vector bundles over M, can be identified with a principal connection in P. Conversely, a principal connection as defined above gives rise to such a section Γ of TP/G.
Finally, let Γ be a principal connection in this sense. Let q:TP→TP/G be the quotient map. The horizontal distribution of the connection is the bundle
Affine property
If ω and ω' are principal connections on a principal bundle P, then the difference ω' - ω is a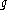-valued 1-form on P which is not only G-equivariant, but horizontal in the sense that it vanishes on any section of the vertical bundle V of P. Hence it is basic and so is determined by a 1-form on M with values in the adjoint bundleAdjoint bundle
In mathematics, an adjoint bundle is a vector bundle naturally associated to any principal bundle. The fibers of the adjoint bundle carry a Lie algebra structure making the adjoint bundle into an algebra bundle...
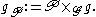
Conversely, any such one form defines (via pullback) a G-equivariant horizontal 1-form on P, and the space of principal G-connections is an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
for this space of 1-forms.
Induced covariant and exterior derivatives
For any linear representation W of G there is an associated vector bundle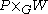 over M, and a principal connection induces a covariant derivativeConnection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
on any such vector bundle. This covariant derivative can be defined using the fact that the space of sections of
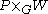over M is isomorphic to the space of G-equivariant W-valued functions on P. More generally, the space of k-forms with values in 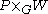is identified with the space of G-equivariant and horizontal W-valued k-forms on P. If α is such a k-form, then its exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
dα, although G-equivariant, is no longer horizontal. However, the combination dα+ωΛα is. This defines an exterior covariant derivative
Exterior covariant derivative
In mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection....
dω from
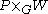-valued k-forms on M to 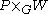-valued (k+1)-forms on M. In particular, when k=0, we obtain a covariant derivative on .Curvature form
The curvature formCurvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
of a principal G-connection ω is the
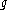-valued 2-form Ω defined byIt is G-equivariant and horizontal, hence corresponds to a 2-form on M with values in
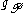. The identification of the curvature with this quantity is sometimes called the second structure equation.Connections on frame bundles and torsion
If the principal bundle P is the frame bundleFrame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
, or (more generally) if it has a solder form
Solder form
In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...
, then the connection is an example of an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, and the curvature is not the only invariant, since the additional structure of the solder form θ, which is an equivariant Rn-valued 1-form on P, should be taken into account. In particular, the torsion form on P, is an Rn-valued 2-form Θ defined by
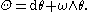
Θ is G-equivariant and horizontal, and so it descends to a tangent-valued 2-form on M, called the torsion. This equation is sometimes called the first structure equation.