
Frame bundle
Encyclopedia
In mathematics
, a frame bundle is a principal fiber bundle F(E) associated to any vector bundle
E. The fiber of F(E) over a point x is the set of all ordered bases, or frames, for Ex. The general linear group
acts naturally on F(E) via a change of basis
, giving the frame bundle the structure of a principal GLk(R)-bundle (where k is the rank of E).
The frame bundle of a smooth manifold is the one associated to its tangent bundle
. For this reason it is sometimes called the tangent frame bundle.
of rank k over a topological space
X. A frame at a point x ∈ X is an ordered basis for the vector space Ex. Equivalently, a frame can be viewed as a linear isomorphism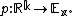
The set of all frames at x, denoted Fx, has a natural right action
by the general linear group
GLk(R) of invertible k×k matrices: a group element g ∈ GLk(R) acts on the frame p via composition
to give a new frame
This action of GLk(R) on Fx is both free and transitive (This follows from the standard linear algebra result that there is a unique invertible linear transformation sending one basis onto another). As a topological space, Fx is homeomorphic to GLk(R) although it lacks a group structure, since there is no "preferred frame". The space Fx is said to be a GLk(R)-torsor.
The frame bundle of E, denoted by F(E) or FGL(E), is the disjoint union
of all the Fx: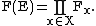
Each point in F(E) is a pair (x, p) where x is a point in X and p is a frame at x. There is a natural projection π : F(E) → X which sends (x, p) to x. The group GLk(R) acts on F(E) on the right as above. This action is clearly free and the orbits are just the fibers of π.
The frame bundle F(E) can be given a natural topology and bundle structure determined by that of E. Let (Ui, φi) be a local trivialization of E. Then for each x ∈ Ui one has a linear isomorphism φi,x : Ex → Rk. This data determines a bijection
given by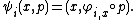
With these bijections, each π−1(Ui) can be given the topology of Ui × GLk(R). The topology on F(E) is the final topology
coinduced by the inclusion maps π−1(Ui) → F(E).
With all of the above data the frame bundle F(E) becomes a principal fiber bundle over X with structure group GLk(R) and local trivializations ({Ui}, {ψi}) One can check that the transition function
s of F(E) are the same as those of E.
The above all works in the smooth category as well: if E is a smooth vector bundle over a smooth manifold M then the frame bundle of E can be given the structure of a smooth principal bundle over M.
s. Each one determines the other. The frame bundle F(E) can be constructed from E as above, or more abstractly using the fiber bundle construction theorem
. With the latter method, F(E) is the fiber bundle with same base, structure group, trivializing neighborhoods, and transition functions as E but with abstract fiber GLk(R), where the action of structure group GLk(R) on the fiber GLk(R) is that of left multiplication.
Given any linear representation ρ : GLk(R) → V there is a vector bundle
associated to F(E) which is given by product F(E) × V modulo the equivalence relation
(pg,v) ~ (p,ρ(g)v) for all g in GLk(R). Denote the equivalence classes by [p,v].
The vector bundle E is naturally isomorphic to the bundle F(E) ×ρ Rk where ρ is the fundamental representation of GLk(R) on Rk. The isomorphism is given by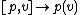
where v is a vector in Rk and p : Rk → Ex is a frame at x. One can easily check that this map is well-defined
.
Any vector bundle associated to E can be given by the above construction. For example, the dual bundle
of E is given by F(E) ×ρ* (Rk)* where ρ* is the dual
of the fundamental representation. Tensor bundle
s of E can be constructed in a similar manner.
of M. The frame bundle of M is often denoted FM or GL(M) rather than F(TM). If M is n-dimensional then the tangent bundle has rank n, so the frame bundle of M is a principal GLn(R) bundle over M.
s of the frame bundle of M are called smooth frames on M. The cross-section theorem for principal bundles states that the frame bundle is trivial over any open set in U in M which admits a smooth frame. Given a smooth frame s : U → FU, the trivialization ψ : FU → U × GLn(R) is given by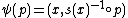
where p is a frame at x. It follows that a manifold is parallelizable if and only if the frame bundle of M admits a global section.
Since the tangent bundle of M is trivializable over coordinate neighborhoods of M so is the frame bundle. In fact, given any coordinate neighborhood U with coordinates (x1,…,xn) the coordinate vector fields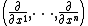
define a smooth frame on U. One of the advantages of working with frame bundles is that they allow one to work with frames other than coordinates frames; one can choose a frame adapted to the problem at hand. This is sometimes called the method of moving frames.
(also known as the fundamental or tautological 1-form). Let x be a point of the manifold M and p a frame at x, so that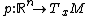
is a linear isomorphism of Rn with the tangent space of M at x. The solder form of FM is the Rn-valued 1-form θ defined by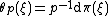
where ξ is a tangent vector to FM at the point (x,p), p-1:TxM → Rn is the inverse of the frame map, and dπ is the differential of the projection map π: FM → M. The solder form is horizontal in the sense that it vanishes on vectors tangent to the fibers of π and right equivariant
in the sense that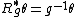
where Rg is right translation by g ∈ GLn(R). A form with these properties is called a basic or tensorial form on FM. Such forms are in 1-1 correspondence with TM-valued 1-forms on M which are, in turn, in 1-1 correspondence with smooth bundle map
s TM → TM over M. Viewed in this light θ is just the identity map
on TM.
. It is then possible to talk about the set of all of orthonormal frame
s for Ex. An orthonormal frame for Ex is an ordered orthonormal basis
for Ex, or, equivalently, a linear isometry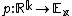
where Rk is equipped with the standard Euclidean metric. The orthogonal group
O(k) acts freely and transitively on the set of all orthonormal frames via right composition. In other words, the set of all orthonormal frames is a right O(k)-torsor.
The orthonormal frame bundle of E, denoted FO(E), is the set of all orthonormal frames at each point x in the base space X. It can be constructed by a method entirely analogous to that of the ordinary frame bundle. The orthonormal frame bundle of a rank k Riemannian vector bundle E → X is a principal O(k)-bundle over X. Again, the construction works just as well in the smooth category.
If the vector bundle E is orientable
then one can define the oriented orthonormal frame bundle of E, denoted FSO(E), as the principal SO(k)-bundle of all positively-oriented orthonormal frames.
If M is an n-dimensional Riemannian manifold
, then the orthonormal frame bundle of M, denoted FOM or O(M), is the orthonormal frame bundle associated to the tangent bundle of M (which is equipped with a Riemannian metric by definition). If M is orientable, then one also has the oriented orthonormal frame bundle FSOM.
Given a Riemannian vector bundle E, the orthonormal frame bundle is a principal O(k)-subbundle
of the general linear frame bundle. In other words, the inclusion map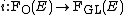
is principal bundle map
. One says that FO(E) is a reduction of the structure group
of FGL(E) from GLk(R) to O(k).
In general, if M is a smooth n-manifold and G is a Lie subgroup
of GLn(R) we define a G-structure
on M to be a reduction of the structure group
of FGL(M) to G. Explicitly, this is a principal G-bundle FG(M) over M together with a G-equivariant bundle map
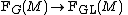
over M.
In this language, a Riemannian metric on M gives rise to an O(n)-structure on M. The following are some other examples.
In many of these instances, a G-structure on M uniquely determines the corresponding structure on M. For example, a SLn(R)-structure on M determines a volume form on M. However, in some cases, such as for symplectic and complex manifolds, an added integrability condition is needed. A Sp2n(R)-structure on M uniquely determines a nondegenerate 2-form on M, but for M to be symplectic, this 2-form must also be closed.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a frame bundle is a principal fiber bundle F(E) associated to any vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
E. The fiber of F(E) over a point x is the set of all ordered bases, or frames, for Ex. The general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
acts naturally on F(E) via a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
, giving the frame bundle the structure of a principal GLk(R)-bundle (where k is the rank of E).
The frame bundle of a smooth manifold is the one associated to its tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. For this reason it is sometimes called the tangent frame bundle.
Definition and construction
Let E → X be a real vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of rank k over a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. A frame at a point x ∈ X is an ordered basis for the vector space Ex. Equivalently, a frame can be viewed as a linear isomorphism
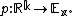
The set of all frames at x, denoted Fx, has a natural right action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GLk(R) of invertible k×k matrices: a group element g ∈ GLk(R) acts on the frame p via composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
to give a new frame

This action of GLk(R) on Fx is both free and transitive (This follows from the standard linear algebra result that there is a unique invertible linear transformation sending one basis onto another). As a topological space, Fx is homeomorphic to GLk(R) although it lacks a group structure, since there is no "preferred frame". The space Fx is said to be a GLk(R)-torsor.
The frame bundle of E, denoted by F(E) or FGL(E), is the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of all the Fx:
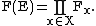
Each point in F(E) is a pair (x, p) where x is a point in X and p is a frame at x. There is a natural projection π : F(E) → X which sends (x, p) to x. The group GLk(R) acts on F(E) on the right as above. This action is clearly free and the orbits are just the fibers of π.
The frame bundle F(E) can be given a natural topology and bundle structure determined by that of E. Let (Ui, φi) be a local trivialization of E. Then for each x ∈ Ui one has a linear isomorphism φi,x : Ex → Rk. This data determines a bijection

given by
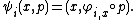
With these bijections, each π−1(Ui) can be given the topology of Ui × GLk(R). The topology on F(E) is the final topology
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
coinduced by the inclusion maps π−1(Ui) → F(E).
With all of the above data the frame bundle F(E) becomes a principal fiber bundle over X with structure group GLk(R) and local trivializations ({Ui}, {ψi}) One can check that the transition function
Transition function
In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
s of F(E) are the same as those of E.
The above all works in the smooth category as well: if E is a smooth vector bundle over a smooth manifold M then the frame bundle of E can be given the structure of a smooth principal bundle over M.
Associated vector bundles
A vector bundle E and its frame bundle F(E) are associated bundleAssociated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
s. Each one determines the other. The frame bundle F(E) can be constructed from E as above, or more abstractly using the fiber bundle construction theorem
Fiber bundle construction theorem
In mathematics, the fiber bundle construction theorem is a theorem which constructs a fiber bundle from a given base space, fiber and a suitable set of transition functions. The theorem also gives conditions under which two such bundles are isomorphic...
. With the latter method, F(E) is the fiber bundle with same base, structure group, trivializing neighborhoods, and transition functions as E but with abstract fiber GLk(R), where the action of structure group GLk(R) on the fiber GLk(R) is that of left multiplication.
Given any linear representation ρ : GLk(R) → V there is a vector bundle

associated to F(E) which is given by product F(E) × V modulo the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
(pg,v) ~ (p,ρ(g)v) for all g in GLk(R). Denote the equivalence classes by [p,v].
The vector bundle E is naturally isomorphic to the bundle F(E) ×ρ Rk where ρ is the fundamental representation of GLk(R) on Rk. The isomorphism is given by
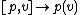
where v is a vector in Rk and p : Rk → Ex is a frame at x. One can easily check that this map is well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
.
Any vector bundle associated to E can be given by the above construction. For example, the dual bundle
Dual bundle
In mathematics, the dual bundle of a vector bundle π : E → X is a vector bundle π* : E* → X whose fibers are the dual spaces to the fibers of E...
of E is given by F(E) ×ρ* (Rk)* where ρ* is the dual
Dual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
of the fundamental representation. Tensor bundle
Tensor bundle
In mathematics, the tensor bundle of a manifold is the direct sum of all tensor products of the tangent bundle and the cotangent bundle of that manifold. To do calculus on the tensor bundle a connection is needed....
s of E can be constructed in a similar manner.
Tangent frame bundle
The tangent frame bundle (or simply the frame bundle) of a smooth manifold M is the frame bundle associated to the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M. The frame bundle of M is often denoted FM or GL(M) rather than F(TM). If M is n-dimensional then the tangent bundle has rank n, so the frame bundle of M is a principal GLn(R) bundle over M.
Smooth frames
Local sectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
s of the frame bundle of M are called smooth frames on M. The cross-section theorem for principal bundles states that the frame bundle is trivial over any open set in U in M which admits a smooth frame. Given a smooth frame s : U → FU, the trivialization ψ : FU → U × GLn(R) is given by
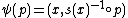
where p is a frame at x. It follows that a manifold is parallelizable if and only if the frame bundle of M admits a global section.
Since the tangent bundle of M is trivializable over coordinate neighborhoods of M so is the frame bundle. In fact, given any coordinate neighborhood U with coordinates (x1,…,xn) the coordinate vector fields
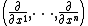
define a smooth frame on U. One of the advantages of working with frame bundles is that they allow one to work with frames other than coordinates frames; one can choose a frame adapted to the problem at hand. This is sometimes called the method of moving frames.
Solder form
The frame bundle of a manifold M is a special type of principal bundle in the sense that its geometry is fundamentally tied to the geometry of M. This relationship can be expressed by means of a vector-valued 1-form on FM called the solder formSolder form
In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...
(also known as the fundamental or tautological 1-form). Let x be a point of the manifold M and p a frame at x, so that
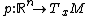
is a linear isomorphism of Rn with the tangent space of M at x. The solder form of FM is the Rn-valued 1-form θ defined by
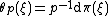
where ξ is a tangent vector to FM at the point (x,p), p-1:TxM → Rn is the inverse of the frame map, and dπ is the differential of the projection map π: FM → M. The solder form is horizontal in the sense that it vanishes on vectors tangent to the fibers of π and right equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
in the sense that
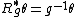
where Rg is right translation by g ∈ GLn(R). A form with these properties is called a basic or tensorial form on FM. Such forms are in 1-1 correspondence with TM-valued 1-forms on M which are, in turn, in 1-1 correspondence with smooth bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
s TM → TM over M. Viewed in this light θ is just the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on TM.
Orthonormal frame bundle
If a vector bundle E is equipped with a Riemannian bundle metric then each fiber Ex is not only a vector space but an inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
. It is then possible to talk about the set of all of orthonormal frame
Orthonormal frame
In Riemannian geometry and relativity theory, an orthonormal frame is a tool for studying the structure of a differentiable manifold equipped with a metric...
s for Ex. An orthonormal frame for Ex is an ordered orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for Ex, or, equivalently, a linear isometry
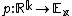
where Rk is equipped with the standard Euclidean metric. The orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(k) acts freely and transitively on the set of all orthonormal frames via right composition. In other words, the set of all orthonormal frames is a right O(k)-torsor.
The orthonormal frame bundle of E, denoted FO(E), is the set of all orthonormal frames at each point x in the base space X. It can be constructed by a method entirely analogous to that of the ordinary frame bundle. The orthonormal frame bundle of a rank k Riemannian vector bundle E → X is a principal O(k)-bundle over X. Again, the construction works just as well in the smooth category.
If the vector bundle E is orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
then one can define the oriented orthonormal frame bundle of E, denoted FSO(E), as the principal SO(k)-bundle of all positively-oriented orthonormal frames.
If M is an n-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, then the orthonormal frame bundle of M, denoted FOM or O(M), is the orthonormal frame bundle associated to the tangent bundle of M (which is equipped with a Riemannian metric by definition). If M is orientable, then one also has the oriented orthonormal frame bundle FSOM.
Given a Riemannian vector bundle E, the orthonormal frame bundle is a principal O(k)-subbundle
Subbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
of the general linear frame bundle. In other words, the inclusion map
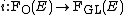
is principal bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
. One says that FO(E) is a reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
of FGL(E) from GLk(R) to O(k).
G-structures
If a smooth manifold M comes with additional structure it is often natural to consider a subbundle of the full frame bundle of M which is adapted to the given structure. For example, if M is a Riemannian manifold we saw above that it is natural to consider the orthonormal frame bundle of M. The orthonormal frame bundle is just a reduction of the structure group of FGL(M) to the orthogonal group O(n).In general, if M is a smooth n-manifold and G is a Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of GLn(R) we define a G-structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
on M to be a reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
of FGL(M) to G. Explicitly, this is a principal G-bundle FG(M) over M together with a G-equivariant bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
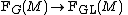
over M.
In this language, a Riemannian metric on M gives rise to an O(n)-structure on M. The following are some other examples.
- Every oriented manifoldOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
has an oriented frame bundle which is just a GLn+(R)-structure on M. - A volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
on M determines a SLn(R)-structure on M. - A 2n-dimensional symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
has a natural Sp2n(R)-structure. - A 2n-dimensional complexComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
or almost complex manifoldAlmost complex manifoldIn mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
has a natural GLn(C)-structure.
In many of these instances, a G-structure on M uniquely determines the corresponding structure on M. For example, a SLn(R)-structure on M determines a volume form on M. However, in some cases, such as for symplectic and complex manifolds, an added integrability condition is needed. A Sp2n(R)-structure on M uniquely determines a nondegenerate 2-form on M, but for M to be symplectic, this 2-form must also be closed.

