Reduction of the structure group
Encyclopedia
In mathematics
, in particular the theory of principal bundle
s, one can ask if a
-bundle "comes from" a subgroup 
. This is called reduction of the structure group (to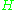 
), and makes sense for any map 
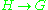, which need not be an inclusion (despite the terminology).
),
a reduction of the structure group (from G to H) is an H-bundle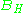
such that the pushout
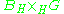is isomorphic to B.
Note that these do not always exist, nor if they exist are they unique.
As a concrete example, every even dimensional real vector space is the underlying real space of a complex vector space: it admits a linear complex structure
. A real vector bundle admits an almost complex structure if and only if it is the underlying real bundle of a complex vector bundle. This is a reduction along the inclusion GL(n,C) → GL(2n,R)
In terms of transition maps, a G-bundle can be reduced if and only if the transition maps can be taken to have values in H.
Note that the term reduction is misleading: it suggests that H is a subgroup of G, which is often the case, but need not be (for example for spin structure
s): it's properly called a lifting
.
More abstractly, "G-bundles over X" is a functor
in G: given a map H → G, one gets a map from H-bundles to G-bundles by inducing
(as above). Reduction of the structure group of a G-bundle B is choosing an H-bundle whose image is B.
The inducing map from H-bundles to G-bundles is in general neither onto nor one-to-one, so the structure group cannot always be reduced, and when it can, this reduction need not be unique. For example, not every manifold is orientable, and those that are orientable admit exactly two orientations.
If H is a Lie subgroup of G, then there is a natural one-to-one correspondence between reductions of a G-bundle B to H and global sections of the fiber bundle
B/H obtained by quotienting B by the right action of H. Specifically, the fibration B → B/H is a principal H-bundle over B/H. If σ : X → B/H is a section, then the pullback bundle
BH = σ−1B is a reduction of B.
s, particularly the tangent bundle
of a manifold
:
, symplectic structure
(as opposed to almost complex structures and almost symplectic structures).
Another example is for a foliation
, which requires a reduction of the tangent bundle
to a block matrix subgroup, together with an integrability condition so that the Frobenius theorem
applies.
BG, and similarly H-bundles are classified by the classifying space BH, and the induced G-structure on an H-bundle corresponds to the induced map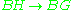
. Thus given a G-bundle with classifying map 
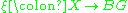, the obstruction to the reduction of the structure group is the class of 
as a map to the cofiber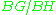 
; the structure group can be reduced if and only if the class of 
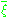is null-homotopic.
When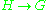
is a homotopy equivalence, the cofiber is contractible, so there is no obstruction to reducing the structure group, for example for 
.
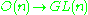Conversely, the cofiber induced by the inclusion of the trivial group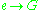
is again 
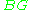, so the obstruction to an absolute parallelism (trivialization of the bundle) is the class of the bundle.
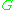-space to an 
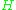-space, thinking of a 
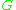-space as a 
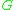-bundle over a point, as in that case the classifying map is null-homotopic, as the domain is a point. Thus there is no obstruction to "reducing the structure group" of a vector space: thus every vector space admits an orientation, and so forth.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular the theory of principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, one can ask if a
-bundle "comes from" a subgroup . This is called reduction of the structure group (to 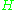), and makes sense for any map 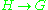, which need not be an inclusion (despite the terminology).Definition
Formally, given a G-bundle B and a map H → G (which need not be an inclusionInclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
),
a reduction of the structure group (from G to H) is an H-bundle
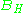such that the pushoutPushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
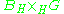is isomorphic to B.Note that these do not always exist, nor if they exist are they unique.
As a concrete example, every even dimensional real vector space is the underlying real space of a complex vector space: it admits a linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
. A real vector bundle admits an almost complex structure if and only if it is the underlying real bundle of a complex vector bundle. This is a reduction along the inclusion GL(n,C) → GL(2n,R)
In terms of transition maps, a G-bundle can be reduced if and only if the transition maps can be taken to have values in H.
Note that the term reduction is misleading: it suggests that H is a subgroup of G, which is often the case, but need not be (for example for spin structure
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
s): it's properly called a lifting
Homotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
.
More abstractly, "G-bundles over X" is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
in G: given a map H → G, one gets a map from H-bundles to G-bundles by inducing
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
(as above). Reduction of the structure group of a G-bundle B is choosing an H-bundle whose image is B.
The inducing map from H-bundles to G-bundles is in general neither onto nor one-to-one, so the structure group cannot always be reduced, and when it can, this reduction need not be unique. For example, not every manifold is orientable, and those that are orientable admit exactly two orientations.
If H is a Lie subgroup of G, then there is a natural one-to-one correspondence between reductions of a G-bundle B to H and global sections of the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
B/H obtained by quotienting B by the right action of H. Specifically, the fibration B → B/H is a principal H-bundle over B/H. If σ : X → B/H is a section, then the pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
BH = σ−1B is a reduction of B.
Examples
Examples for vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, particularly the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
:
-
is an orientation, and this is possible if and only if the bundle is orientable -
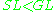is a volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
; since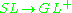
is a deformation retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
, a volume form exists if and only if a bundle is orientable -
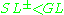is a pseudo-volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
, and this is always possible -
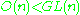is a Riemannian metric; as 
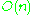is the maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
(so the inclusion is a deformation retract), this is always possible -
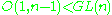is a pseudo-Riemannian metric; there is the topological obstruction to this reduction -
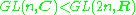is an almost complex structureAlmost complex manifoldIn mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost... -
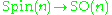(which is not an inclusion: it's a 2-fold covering space) is a spin structure. -
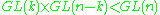decomposes a vector bundle as a Whitney sum (direct sum) of sub-bundles of rank k and n − k.
Integrability
Many geometric structures are stronger than G-structures; they are G-structures with an integrability condition. Thus such a structure requires a reduction of the structure group (and can be obstructed, as below), but this is not sufficient. Examples include complex structureComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
, symplectic structure
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
(as opposed to almost complex structures and almost symplectic structures).
Another example is for a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
, which requires a reduction of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
to a block matrix subgroup, together with an integrability condition so that the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
applies.
Obstruction
G-bundles are classified by the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG, and similarly H-bundles are classified by the classifying space BH, and the induced G-structure on an H-bundle corresponds to the induced map
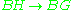. Thus given a G-bundle with classifying map 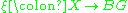, the obstruction to the reduction of the structure group is the class of as a map to the cofiber 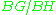; the structure group can be reduced if and only if the class of 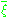is null-homotopic.When
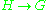is a homotopy equivalence, the cofiber is contractible, so there is no obstruction to reducing the structure group, for example for 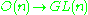.Conversely, the cofiber induced by the inclusion of the trivial group
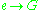is again 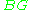, so the obstruction to an absolute parallelism (trivialization of the bundle) is the class of the bundle.Structure over a point
As a simple example, there is no obstruction to reducing the structure group of a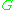-space to an 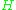-space, thinking of a 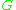-space as a -bundle over a point, as in that case the classifying map is null-homotopic, as the domain is a point. Thus there is no obstruction to "reducing the structure group" of a vector space: thus every vector space admits an orientation, and so forth.