Maximal compact subgroup
Encyclopedia
In mathematics
, a maximal compact subgroup K of a topological group
G is a subgroup
K that is a compact space
, in the subspace topology
, and maximal
amongst such subgroups.
Maximal compact subgroups play an important role in the classification of Lie groups and especially semi-simple Lie groups. Maximal compact subgroups of Lie groups are not in general unique, but are unique up to conjugation – they are essentially unique
.
, inside the general linear group
GL(2, R). A related example is the circle group SO(2) inside SL(2, R). Evidently SO(2) inside GL(2, R) is compact and not maximal. The non-uniqueness of these examples can be seen as any inner product has an associated orthogonal group, and the essential uniqueness corresponds to the essential uniqueness of the inner product.
that happens to be compact; which would probably be called a compact (maximal subgroup), but in any case is not the intended meaning (and in fact maximal proper subgroups are not in general compact).
and 
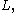there is an element 
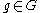such that 
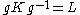– hence a maximal compact subgroup is essentially unique
, and people often speak of "the" maximal compact subgroup.
For the example of the general linear group GL(n,R), this corresponds to the fact that any inner product on R^n defines a (compact) orthogonal group (its isometry group) – and that it admits a orthonormal basis: the change of basis defines the conjugating element conjugating the isometry group to the classical orthogonal group O(n,R).
when G is not compact. In that case a maximal compact subgroup K is a compact Lie group (since a closed subgroup of a Lie group is a Lie group), for which the theory is easier.
The operations relating the representation theories of G and K are restricting representations
from G to K, and inducing representations
from K to G,, and these are quite well understood; their theory includes that of spherical function
s.
of the Lie groups is also largely carried by a maximal compact subgroup K. To be precise, a connected Lie group is a topological product (though not a group theoretic product!) of a maximal compact K and a Euclidean space –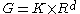
– thus in particular K is a deformation retract
of G, and is homotopy equivalent, and thus they have the same homotopy groups. Indeed, the inclusion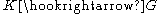
and the deformation retraction 
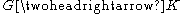are homotopy equivalences.
For the general linear group, this decomposition is the QR decomposition
, and the deformation retraction is the Gram-Schmidt process. For a general semisimple Lie group, the decomposition is the Iwasawa decomposition
of G as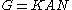
in which K occurs in a product with a contractible subgroup 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a maximal compact subgroup K of a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
K that is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, in the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
, and maximal
Maximal
Maximal may refer to:*Maximal element, a mathematical definition*Maximal , a faction of Transformers*Maximalism, an artistic style*Maximal set*Maxim , a men's magazine marketed as Maximal in several countriesSee also...
amongst such subgroups.
Maximal compact subgroups play an important role in the classification of Lie groups and especially semi-simple Lie groups. Maximal compact subgroups of Lie groups are not in general unique, but are unique up to conjugation – they are essentially unique
Essentially unique
In mathematics, the term essentially unique is used to indicate that while some object is not the only one that satisfies certain properties, all such objects are "the same" in some sense appropriate to the circumstances...
.
Example
An example would be the subgroup O(2), the orthogonal groupOrthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, inside the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(2, R). A related example is the circle group SO(2) inside SL(2, R). Evidently SO(2) inside GL(2, R) is compact and not maximal. The non-uniqueness of these examples can be seen as any inner product has an associated orthogonal group, and the essential uniqueness corresponds to the essential uniqueness of the inner product.
Definition
A maximal compact subgroup is a maximal subgroup amongst compact subgroups – a maximal (compact subgroup) – rather than being (alternate possible reading) a maximal subgroupMaximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
that happens to be compact; which would probably be called a compact (maximal subgroup), but in any case is not the intended meaning (and in fact maximal proper subgroups are not in general compact).
Existence
The Cartan-Iwasawa-Malcev theorem asserts that every connected Lie group (and indeed every connected locally compact group) admits maximal compact subgroups and that they are all conjugate to one another. For a semisimple Lie group this is a consequence of the Cartan fixed point theorem.Uniqueness
Maximal compact subgroups of connected Lie groups are usually not unique, but they are unique up to conjugation, meaning that given two maximal compact subgroups and 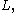there is an element 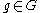such that 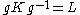– hence a maximal compact subgroup is essentially uniqueEssentially unique
In mathematics, the term essentially unique is used to indicate that while some object is not the only one that satisfies certain properties, all such objects are "the same" in some sense appropriate to the circumstances...
, and people often speak of "the" maximal compact subgroup.
For the example of the general linear group GL(n,R), this corresponds to the fact that any inner product on R^n defines a (compact) orthogonal group (its isometry group) – and that it admits a orthonormal basis: the change of basis defines the conjugating element conjugating the isometry group to the classical orthogonal group O(n,R).
Representation theory
Maximal compact subgroups play a basic role in the representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
when G is not compact. In that case a maximal compact subgroup K is a compact Lie group (since a closed subgroup of a Lie group is a Lie group), for which the theory is easier.
The operations relating the representation theories of G and K are restricting representations
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
from G to K, and inducing representations
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
from K to G,, and these are quite well understood; their theory includes that of spherical function
Spherical function
Spherical function can refer to* Spherical harmonics*Zonal spherical function...
s.
Topology
The algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
of the Lie groups is also largely carried by a maximal compact subgroup K. To be precise, a connected Lie group is a topological product (though not a group theoretic product!) of a maximal compact K and a Euclidean space –
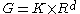– thus in particular K is a deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of G, and is homotopy equivalent, and thus they have the same homotopy groups. Indeed, the inclusion
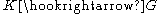and the deformation retraction 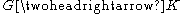are homotopy equivalences.For the general linear group, this decomposition is the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
, and the deformation retraction is the Gram-Schmidt process. For a general semisimple Lie group, the decomposition is the Iwasawa decomposition
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
of G as
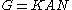in which K occurs in a product with a contractible subgroup .