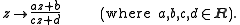SL2(R)
Encyclopedia
In mathematics
, the special linear group
SL(2,R) or SL2(R) is the group
of all real 2 × 2 matrices
with determinant
one:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,R) or SL2(R) is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all real 2 × 2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
one:
-

It is a simpleSimple Lie groupIn group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
real Lie group with applications in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, and physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
SL(2,R) acts on the complex upper half-plane by fractional linear transformations. The action factors through the quotientQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
PSL(2,R) (the 2 × 2 projective special linear group over R). More specifically,- PSL(2,R) = SL(2,R)/{±I},
where I denotes the 2 × 2 identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. It contains the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
PSL(2,Z).
Also closely related is the 2-fold covering group, Mp(2,R), a metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
(thinking of SL(2,R) as a symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
).
Another related group is SL±(2,R) the group of real 2 × 2 matrices with determinant ±1; this is more commonly used in the context of the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, however.
Descriptions
SL(2,R) is the group of all linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of R2 that preserve orientedOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
area. It is isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(2,R) and the generalized special unitary groupSpecial unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(1,1). It is also isomorphic to the group of unit-length coquaternions. The group SL±(2,R) preserves unoriented area: it may reverse orientation.
The quotient PSL(2,R) has several interesting descriptions:- It is the group of orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-preserving projective transformations of the real projective line R∪{∞}. - It is the group of conformalConformal mapIn mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of the unit disc. - It is the group of orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-preserving isometriesIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the hyperbolic planeHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. - It is the restricted Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
of three-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. Equivalently, it is isomorphic to the indefinite orthogonal group SO+(1,2). It follows that SL(2,R) is isomorphic to the spin group Spin(2,1)+.
Elements of the modular group PSL(2,Z) have additional interpretations, as do elements of the group SL(2,Z) (as linear transforms of the torus), and these interpretations can also be viewed in light of the general theory of SL(2,R).
Linear fractional transformations
Elements of PSL(2,R) act on the real projective line R∪{∞} as linear fractional transformations:
This is analogous to the action of PSL(2,C) on the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
by Möbius transformations. It is the restriction of the action of PSL(2,R) on the hyperbolic plane to the boundary at infinity.
Möbius transformations
Elements of PSL(2,R) act on the complex plane by Möbius transformations:
This is precisely the set of Möbius transformations that preserve the upper half-plane. It follows that PSL(2,R) is the group of conformal automorphisms of the upper half-plane. By the Riemann mapping theorem, it is also the group of conformal automorphisms of the unit disc.
These Möbius transformations act as the isometries of the upper half-plane modelPoincaré half-plane modelIn non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
of hyperbolic space, and the corresponding Möbius transformations of the disc are the hyperbolic isometries of the Poincaré disk modelPoincaré disk modelIn geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
.
Adjoint representation
The group SL(2,R) acts on its Lie algebra sl(2,R) by conjugation (remember that the Lie algebra elements are also 2 by 2 matrices), yielding a faithful 3-dimensional linear representationRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of PSL(2,R). This can alternatively be described as the action of PSL(2,R) on the space of quadratic forms on R2. The result is the following representation: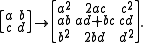
The Killing formKilling formIn mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
on sl(2,R) has signatureMetric signatureThe signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(2,1), and induces an isomorphism between PSL(2,R) and the Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
SO+(2,1). This action of PSL(2,R) on Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
restricts to the isometric action of PSL(2,R) on the hyperboloid modelHyperboloid modelIn geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
of the hyperbolic plane.
Classification of elements
The eigenvalues of an element A ∈ SL(2,R) satisfy the characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....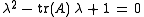
and therefore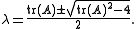
This leads to the following classification of elements, with corresponding action on the Euclidean plane:- If | tr(A) | < 2, then A is called elliptic, and is conjugate to a rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. - If | tr(A) | = 2, then A is called parabolic, and is a shear mapping.
- If | tr(A) | > 2, then A is called hyperbolic, and is a squeeze mappingSqueeze mappingIn linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
.
The names correspond to the classification of conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s by eccentricityEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
: if one defines eccentricity as half the absolute value of the trace (ε = ½ tr; dividing by 2 corrects for the effect of dimension, while absolute value corresponds to ignoring an overall factor of ±1 such as when working in PSL(2, R)), then this yields: , elliptic;
, elliptic; 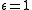 , parabolic;
, parabolic; 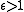 , hyperbolic.
, hyperbolic.
The identity element 1 and negative identity element -1 (in PSL(2,R) they are the same), have trace ±2, and hence by this classification are parabolic elements, though they are often considered separately.
The same classification is used for SL(2,C) and PSL(2,C) (Möbius transformations) and PSL(2,R) (real Möbius transformations), with the addition of "loxodromic" transformations corresponding to complex traces; analogous classifications are used elsewhere.
A subgroup that is contained with the elliptic (respectively, parabolic, hyperbolic) elements, plus the identity and negative identity, is called an elliptic subgroup (respectively, parabolic subgroup, hyperbolic subgroup).
This is a classification into subsets, not subgroups: these sets are not closed under multiplication (the product of two parabolic elements need not be parabolic, and so forth). However, all elements are conjugate into one of 3 standard one-parameter subgroups (possibly times ±1), as detailed below.
Topologically, as trace is a continuous map, the elliptic elements (excluding ±1) are an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, as are the hyperbolic elements (excluding ±1), while the parabolic elements (including ±1) are a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
Elliptic elements
The eigenvalues for an elliptic element are both complex, and are conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
values on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. Such an element is conjugate to a rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of the Euclidean plane – they can be interpreted as rotations in a possibly non-orthogonal basis – and the corresponding element of PSL(2,R) acts as (conjugate to) a rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of the hyperbolic plane and of Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
Elliptic elements of the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
must have eigenvalues {ω, ω-1}, where ω is a primitive 3rd, 4th, or 6th root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. These are all the elements of the modular group with finite orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
, and they act on the torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
as periodic diffeomorphisms.
Elements of trace 0 may be called "circular elements" (by analogy with eccentricity) but this is rarely done; they correspond to elements with eigenvalues ±i, and are conjugate to rotation by 90°, and square to -I: they are the non-identity involutions in PSL(2).
Elliptic elements are conjugate into the subgroup of rotations of the Euclidean plane, the special orthogonal group SO(2); the angle of rotation is arccosArccosArccos may refer to:*arccos is an inverse trigonometric function of cosine*ARccOS Protection is a copyright protection mechanism by Sony...
of half of the trace, with the sign of the rotation determined by orientation. (A rotation and its inverse are conjugate in GL(2) but not SL(2).)
Parabolic elements
A parabolic element has only a single eigenvalue, which is either 1 or -1. Such an element acts as a shear mapping on the Euclidean plane, and the corresponding element of PSL(2,R) acts as a limit rotation of the hyperbolic plane and as a null rotation of Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
Parabolic elements of the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
act as Dehn twistDehn twistIn geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface .-Definition:...
s of the torus.
Parabolic elements are conjugate into the 2 component group of standard shears × ±I: . In fact, they are all conjugate (in SL(2)) to one of the four matrices
. In fact, they are all conjugate (in SL(2)) to one of the four matrices 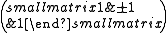 ,
, 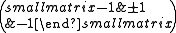 (in GL(2) or SL±(2), the ± can be omitted, but in SL(2) it cannot).
(in GL(2) or SL±(2), the ± can be omitted, but in SL(2) it cannot).
Hyperbolic elements
The eigenvalues for a hyperbolic element are both real, and are reciprocals. Such an element acts as a squeeze mappingSqueeze mappingIn linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
of the Euclidean plane, and the corresponding element of PSL(2,R) acts as a translationTranslationTranslation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
of the hyperbolic plane and as a Lorentz boostLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
on Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
Hyperbolic elements of the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
act as Anosov diffeomorphismAnosov diffeomorphismIn mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
s of the torus.
Hyperbolic elements are conjugate into the 2 component group of standard squeezes × ±I: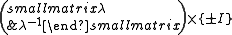 ; the hyperbolic angleHyperbolic angleIn mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
; the hyperbolic angleHyperbolic angleIn mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
of the hyperbolic rotation is given by arcosh of half of the trace, but the sign can be positive or negative: in contrast to the elliptic case, a squeeze and its inverse are conjugate in SL₂ (by a rotation in the axes; for standard axes, a rotation by 90°).
Conjugacy classes
By Jordan normal formJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
, matrices are classified up to conjugacy (in GL(n,C)) by eigenvalues and nilpotence (concretely, nilpotence means where 1s occur in the Jordan blocks). Thus elements of SL(2) are classified up to conjugacy in GL(2) (or indeed SL±(2)) by trace (since determinant is fixed, and trace and determinant determine eigenvalues), except if the eigenvalues are equal, so ±I and the parabolic elements of trace +2 and trace 2 are not conjugate (the former have no off-diagonal entries in Jordan form, while the latter do).
Up to conjugacy in SL(2) (instead of GL(2)), there is an additional datum, corresponding to orientation: a clockwise and counterclockwise (elliptical) rotation are not conjugate, nor are a positive and negative shear, as detailed above; thus for absolute value of trace less than 2, there are two conjugacy classes for each trace (clockwise and counterclockwise rotations), for absolute value of the trace equal to 2 there are three conjugacy classes for each trace (positive shear, identity, negative shear; and the negatives of these), and for absolute value of the trace greater than 2 there is one conjugacy class for a given trace.
Topology and universal cover
As a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, PSL(2,R) can be described as the unit tangent bundleUnit tangent bundleIn Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
of the hyperbolic plane. It is a circle bundle, and has a natural contact structure induced by the symplectic structureSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
on the hyperbolic plane. SL(2,R) is a 2-fold cover of PSL(2,R), and can be thought of as the bundle of spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s on the hyperbolic plane.
The fundamental group of SL(2,R) is the infinite cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z. The universal covering group, denoted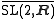 , is an example of a finite-dimensional Lie group that is not a matrix groupMatrix groupIn mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
, is an example of a finite-dimensional Lie group that is not a matrix groupMatrix groupIn mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
. That is, admits no faithfulFaithful representationIn mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
admits no faithfulFaithful representationIn mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
, finite-dimensional representationGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
.
As a topological space,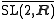 is a line bundle over the hyperbolic plane. When imbued with a left-invariant metric, the 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
is a line bundle over the hyperbolic plane. When imbued with a left-invariant metric, the 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
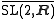 becomes one of the eight Thurston geometries. For example,
becomes one of the eight Thurston geometries. For example, 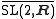 is the universal cover of the unit tangent bundle to any hyperbolic surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is the universal cover of the unit tangent bundle to any hyperbolic surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
. Any manifold modeled on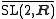 is orientable, and is a circle bundle over some 2-dimensional hyperbolic orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
is orientable, and is a circle bundle over some 2-dimensional hyperbolic orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
(a Seifert fiber spaceSeifert fiber spaceA Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
).
Under this covering, the preimage of the modular group PSL(2,Z) is the braid group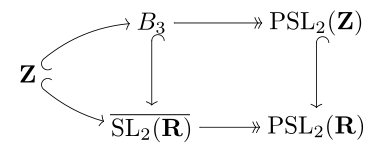 Braid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
Braid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
on 3 generators, B3, which is the universal central extension of the modular group. These are lattices inside the relevant algebraic groups, and this corresponds algebraically to the universal covering group in topology.
The 2-fold covering group can be identified as Mp(2,R), a metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
, thinking of SL(2,R) as the symplectic group Sp(2,R).
The aforementioned groups together form a sequence: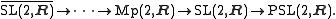
However, there are other covering groups of PSL(2,R) corresponding to all n, as n Z < Z ≅ π1 (PSL(2,R)), which form a lattice of covering groups by divisibility; these cover SL(2,R) if and only if n is even.
Algebraic structure
The centerCenter (group theory)In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of SL(2,R) is the two-element group {±1}, and the quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
PSL(2,R) is simpleSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
.
Discrete subgroups of PSL(2,R) are called Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s. These are the hyperbolic analogue of the Euclidean wallpaper groupWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s and Frieze groupFrieze groupA frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s. The most famous of these is the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
PSL(2,Z), which acts on a tessellation of the hyperbolic plane by ideal triangles.
The circle group SO(2)Orthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
is a maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of SL(2,R), and the circle SO(2)/{±1} is a maximal compact subgroup of PSL(2,R).
The Schur multiplierSchur multiplierIn mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
of the discrete group PSL(2,R) is much larger than ZIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, and the universal central extension is much larger than the universal covering group. However these large central extensions do not take the topology into account and are somewhat pathological.
Representation theory
SL(2,R) is a real, non-compact simple Lie groupSimple Lie groupIn group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
, and is the split-real form of the complex Lie group SL(2,C). The Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SL(2,R), denoted sl(2,R), is the algebra of all real, tracelessTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
2 × 2 matrices. It is the Bianchi algebraBianchi classificationIn mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
of type VIII.
The finite-dimensional representation theory of SL(2,R) is equivalent to the representation theory of SU(2)Representation theory of SU(2)In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...
, which is the compact real form of SL(2,C). In particular, SL(2,R) has no nontrivial finite-dimensional unitary representations.
The infinite-dimensional representation theory of SL(2,R) is quite interesting. The group has several families of unitary representations, which were worked out in detail by GelfandIsrael GelfandIsrael Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and NaimarkMark NaimarkMark Aronovich Naimark was a Soviet mathematician.He was born in Odessa, Russian Empire into a Jewish family and died in Moscow, USSR...
(1946), V. Bargmann (1947), and Harish-ChandraHarish-ChandraHarish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
(1952).
See also
- linear group
- special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
- projective linear groupProjective linear groupIn mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
- hyperbolic isometry
- modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
- Möbius transformation
- projective transformation
- Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
- Table of Lie groupsTable of Lie groupsThis article gives a table of some common Lie groups and their associated Lie algebras.The following are noted: the topological properties of the group , as well as on their algebraic properties .For more examples of Lie groups and other...
- Anosov flow