
Center (group theory)
Encyclopedia
In abstract algebra
, the center of a group
G, denoted Z(G),The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation
,
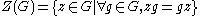 .
.
The center is a subgroup
of G, which by definition is abelian
(that is commutative). As a subgroup, it is always normal
, and indeed characteristic
, but it need not be fully characteristic
. The quotient group
G / Z(G) is isomorphic
to the group of inner automorphism
s of G.
A group G is abelian if and only if Z(G) = G. At the other extreme, a group is said to be centerless if Z(G) is trivial, i.e. consists only of the identity element
.
The elements of the center are sometimes called central.
of G. In particular:
Furthermore the center of G is always a normal subgroup
of G, as it is closed under conjugation
.
 .
.
This is a group homomorphism
, and its kernel
is precisely the center of G, and its image is called the inner automorphism group of G, denoted Inn(G). By the first isomorphism theorem we get
The cokernel
of this map is the group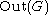 of outer automorphisms, and these form the exact sequence
of outer automorphisms, and these form the exact sequence

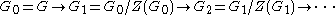
The kernel of the map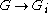 is the ith center of G (second center, third center, etc.), and is denoted
is the ith center of G (second center, third center, etc.), and is denoted  Concretely, the
Concretely, the  -st center are the terms that commute with all elements up to an element of the ith center. Following this definition, one can define the 0th center of a group to be the identity subgroup. This can be continued to transfinite ordinals by transfinite induction
-st center are the terms that commute with all elements up to an element of the ith center. Following this definition, one can define the 0th center of a group to be the identity subgroup. This can be continued to transfinite ordinals by transfinite induction
; the union of all the higher centers is called the hypercenter.This union will include transfinite terms if the UCS does not stabilize at a finite stage.
The ascending chain of subgroups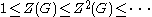
stabilizes at i (equivalently, ) if and only if
) if and only if
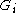 is centerless.
is centerless.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the center of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G, denoted Z(G),The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
,
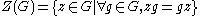 .
.The center is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G, which by definition is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(that is commutative). As a subgroup, it is always normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, and indeed characteristic
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
, but it need not be fully characteristic
Fully characteristic subgroup
In mathematics, a subgroup of a group is fully characteristic if it is invariant under every endomorphism of the group. That is, any endomorphism of the group takes elements of the subgroup to elements of the subgroup....
. The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G / Z(G) is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the group of inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s of G.
A group G is abelian if and only if Z(G) = G. At the other extreme, a group is said to be centerless if Z(G) is trivial, i.e. consists only of the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
The elements of the center are sometimes called central.
As a subgroup
The center of G is always a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. In particular:
- Z(G) contains e, the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G, because eg = g = ge for all g ∈ G by definition of e, so by definition of Z(G), e ∈ Z(G); - If x and y are in Z(G), then (xy)g = x(yg) = x(gy) = (xg)y = (gx)y = g(xy) for each g ∈ G, and so xy is in Z(G) as well (i.e., Z(G) exhibits closure);
- If x is in Z(G), then gx = xg, and multiplying twice, once on the left and once on the right, by x−1, gives x−1g = gx−1 — so x−1 ∈ Z(G).
Furthermore the center of G is always a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G, as it is closed under conjugation
Conjugate closure
In group theory, the conjugate closure of a subset S of a group G is the subgroup of G generated by SG, i.e. the closure of SG under the group operation, where SG is the conjugates of the elements of S:The conjugate closure of S is denoted or G.The conjugate closure of any subset S of a group G...
.
Conjugation
Consider the map f: G → Aut(G) from G to the automorphism group of G defined by f(g) = φg, where φg is the automorphism of G defined by .
.This is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, and its kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is precisely the center of G, and its image is called the inner automorphism group of G, denoted Inn(G). By the first isomorphism theorem we get

The cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of this map is the group
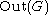 of outer automorphisms, and these form the exact sequence
of outer automorphisms, and these form the exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...

Examples
- The center of an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
G is all of G. - The center of a nonabelianNonabelian groupIn mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
simple groupSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
is trivial. - The center of the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dn is trivial when n is odd. When n is even, the center consists of the identity element together with the 180° rotation of the polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
. - The center of the quaternion groupQuaternion groupIn group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
 is
is  .
. - The center of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn is trivial for n ≥ 3. - The center of the alternating group An is trivial for n ≥ 4.
- The center of the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
 is the collection of scalar matricesDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
is the collection of scalar matricesDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
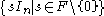 .
. - The center of the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
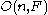 is
is  .
. - The center of the multiplicative group of non-zero quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s is the multiplicative group of non-zero real numbers. - Using the class equation one can prove that the center of any non-trivial finiteFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
p-groupP-groupIn mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
is non-trivial. - If the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
 is cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
is cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, G is abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(and so G = Z(G), and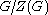 is trivial).
is trivial).
Higher centers
Quotienting out by the center of a group yields a sequence of groups called the upper central series: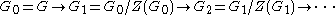
The kernel of the map
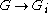 is the ith center of G (second center, third center, etc.), and is denoted
is the ith center of G (second center, third center, etc.), and is denoted  Concretely, the
Concretely, the  -st center are the terms that commute with all elements up to an element of the ith center. Following this definition, one can define the 0th center of a group to be the identity subgroup. This can be continued to transfinite ordinals by transfinite induction
-st center are the terms that commute with all elements up to an element of the ith center. Following this definition, one can define the 0th center of a group to be the identity subgroup. This can be continued to transfinite ordinals by transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
; the union of all the higher centers is called the hypercenter.This union will include transfinite terms if the UCS does not stabilize at a finite stage.
The ascending chain of subgroups
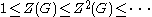
stabilizes at i (equivalently,
 ) if and only if
) if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
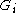 is centerless.
is centerless.Examples
- For a centerless group, all higher centers are zero, which is the case
 of stabilization.
of stabilization. - By Grün's lemma, the quotient of a perfect groupPerfect groupIn mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
by its center is centerless, hence all higher centers equal the center. This is a case of stabilization at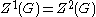 .
.

