Perfect group
Encyclopedia
In mathematics
, more specifically in the area of modern algebra known as group theory
, a group
is said to be perfect if it equals its own commutator subgroup
, or equivalently, if the group has no nontrivial abelian
quotients
(equivalently, its abelianization, which is the universal abelian quotient, is trivial). In symbols, a perfect group is one such that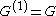
(the commutator subgroup equals the group), or equivalently one such that 
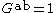(its abelianization is trivial).
simple group
is perfect since the commutator subgroup is a normal subgroup
with abelian quotient. Conversely, a perfect group need not be simple; for example, the special linear group
SL(2,5) (or the binary icosahedral group which is isomorphic to it) is perfect but not simple (it has a non-trivial center containing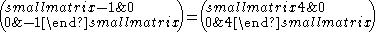
).
More generally, a quasisimple group
(a perfect central extension of a simple group) which is a non-trivial extension (i.e., not a simple group itself) is perfect but not simple; this includes all the insoluble non-simple finite special linear groups SL(n,q) as extensions of the projective special linear group PSL(n,q) (SL(2,5) is an extension of PSL(2,5), which is isomorphic to A5). Similarly, the special linear group over the real and complex numbers is perfect, but the general linear group GL is never perfect (except when trivial or over F2, where it equals the special linear group), as the determinant
gives a non-trivial abelianization and indeed the commutator subgroup is SL.
A non-trivial perfect group, however, is necessarily not solvable
.
Every acyclic group is perfect, but the converse is not true: A5 is perfect but not acyclic (in fact, not even superperfect
), see . In fact, for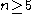
the alternating group 
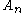is perfect but not superperfect, with 
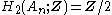for 
.
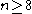of a perfect group by its center
is centerless (has trivial center).
I.e., if Z(G) denotes the center of a given group G, and G is perfect, then the center of the quotient group G ⁄ Z(G) is the trivial group
:
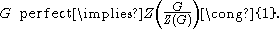
Proof
If G is a perfect group, let Z1 and Z2 denote the first two terms of the upper central series of G (i.e., Z1 is the center of G, and Z2/Z1 is the center of G/Z1). If H and K are subgroups of G, denote the commutator
of H and K by [H,K] and note that [Z1,G] = 1 and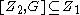
, and consequently (the convention that [X,Y,Z] = i>X,Y],Z] is followed):
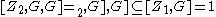
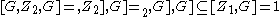
By the three subgroups lemma
(or equivalently, by the Hall-Witt identity), it follows that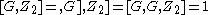
. Therefore, 
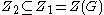, and the center of the quotient group G ⁄ Z(G) is the trivial group
.
As a consequence, all higher centers (that is, higher terms in the upper central series) of a perfect group equal the center.
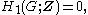as the first homology group of a group is exactly the abelianization of the group, and perfect means trivial abelianization. An advantage of this definition is that it admits strengthening:
, a group is said to be quasi-perfect if its commutator subgroup is perfect; in symbols, a quasi-perfect group is one such that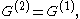
(the commutator of the commutator subgroup is the commutator subgroup), while a perfect group is one such that 
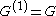(the commutator subgroup is the whole group). See and .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the area of modern algebra known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is said to be perfect if it equals its own commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
, or equivalently, if the group has no nontrivial abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
quotients
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
(equivalently, its abelianization, which is the universal abelian quotient, is trivial). In symbols, a perfect group is one such that
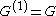(the commutator subgroup equals the group), or equivalently one such that 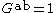(its abelianization is trivial).Examples
The smallest (non-trivial) perfect group is the alternating group A5. More generally, any non-abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
is perfect since the commutator subgroup is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
with abelian quotient. Conversely, a perfect group need not be simple; for example, the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,5) (or the binary icosahedral group which is isomorphic to it) is perfect but not simple (it has a non-trivial center containing
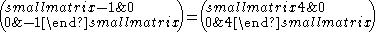).More generally, a quasisimple group
Quasisimple group
In mathematics, a quasisimple group is a group that is a perfect central extension E of a simple group S...
(a perfect central extension of a simple group) which is a non-trivial extension (i.e., not a simple group itself) is perfect but not simple; this includes all the insoluble non-simple finite special linear groups SL(n,q) as extensions of the projective special linear group PSL(n,q) (SL(2,5) is an extension of PSL(2,5), which is isomorphic to A5). Similarly, the special linear group over the real and complex numbers is perfect, but the general linear group GL is never perfect (except when trivial or over F2, where it equals the special linear group), as the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
gives a non-trivial abelianization and indeed the commutator subgroup is SL.
A non-trivial perfect group, however, is necessarily not solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
Every acyclic group is perfect, but the converse is not true: A5 is perfect but not acyclic (in fact, not even superperfect
Superperfect group
In mathematics, in the realm of group theory, a group is said to be superperfect when its first two homology groups are trivial: H_1=H_2=0. This is stronger than a perfect group, which is one whose first homology group vanishes...
), see . In fact, for
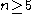the alternating group 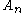is perfect but not superperfect, with 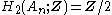for 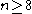.Grün's lemma
A basic fact about perfect groups is Grün's lemma from : the quotientQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a perfect group by its center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
is centerless (has trivial center).
I.e., if Z(G) denotes the center of a given group G, and G is perfect, then the center of the quotient group G ⁄ Z(G) is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
:
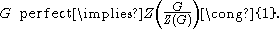
Proof
If G is a perfect group, let Z1 and Z2 denote the first two terms of the upper central series of G (i.e., Z1 is the center of G, and Z2/Z1 is the center of G/Z1). If H and K are subgroups of G, denote the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of H and K by [H,K] and note that [Z1,G] = 1 and
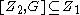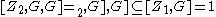
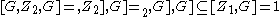
, and consequently (the convention that [X,Y,Z] = i>X,Y],Z] is followed):By the three subgroups lemma
Three subgroups lemma
In mathematics, more specifically group theory, the three subgroups lemma is a result concerning commutators. It is a consequence of the Hall–Witt identity.-Notation:In that which follows, the following notation will be employed:...
(or equivalently, by the Hall-Witt identity), it follows that
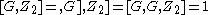. Therefore, 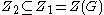, and the center of the quotient group G ⁄ Z(G) is the trivial groupTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
As a consequence, all higher centers (that is, higher terms in the upper central series) of a perfect group equal the center.
Group homology
In terms of group homology, a perfect group is precisely one whose first homology group vanishes: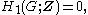 as the first homology group of a group is exactly the abelianization of the group, and perfect means trivial abelianization. An advantage of this definition is that it admits strengthening:
- A superperfect groupSuperperfect groupIn mathematics, in the realm of group theory, a group is said to be superperfect when its first two homology groups are trivial: H_1=H_2=0. This is stronger than a perfect group, which is one whose first homology group vanishes...
is one whose first two homology groups vanishes: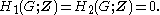
- An acyclic group is one all of whose (reduced) homology groups vanish
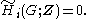(This is equivalent to all homology groups other than 
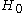vanishing.)
Quasi-perfect group
Especially in the field of algebraic K-theoryAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, a group is said to be quasi-perfect if its commutator subgroup is perfect; in symbols, a quasi-perfect group is one such that
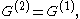(the commutator of the commutator subgroup is the commutator subgroup), while a perfect group is one such that 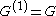(the commutator subgroup is the whole group). See and .