Schur multiplier
Encyclopedia
In mathematical group theory
, the Schur multiplier or Schur multiplicator is the second homology group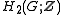
of a group G.
It was introduced by in his work on projective representation
s.
whose exponent
divides the order of G. If a Sylow p-subgroup of G is cyclic for some p, then order of M(G) is not divisible by p.
In particular, if all Sylow p-subgroups of G are cyclic, then M(G) is trivial.
For instance, the Schur multiplier of the nonabelian group of order 6 is the trivial group
since every Sylow subgroup is cyclic. The Schur multiplier of the elementary abelian group
of order 16 is an elementary abelian group of order 64, showing that the multiplier can be strictly larger than the group itself. The Schur multiplier of the quaternion group
is trivial, but the Schur multiplier of dihedral 2-groups
has order 2.
The Schur multipliers of the finite simple group
s are given at the list of finite simple groups. The covering groups of the alternating and symmetric groups
are of considerable recent interest.
s of a group, and the modern formulation of his definition is the second cohomology group
H2(G,C×). A projective representation is much like a group representation
except that instead of a homomorphism into the general linear group
GL(n,C), one takes a homomorphism into the projective general linear group PGL(n,C). In other words, a projective representation is a representation modulo the center.
showed that every finite group G has associated to it at least one finite group C, called a Schur cover, with the property that every projective representation of G can be lifted to an ordinary representation of C. The Schur cover is also known as a covering group or Darstellungsgruppe. The Schur covers of the finite simple groups are known, and each is an example of a quasisimple group
. The Schur cover of a perfect group
is uniquely determined up to isomorphism, but the Schur cover of a general finite group is only determined up to isoclinism.
A central extension of a group G is an extension
where K ≤ Z(C) is a subgroup
of the center
of C.
A stem extension of a group G is an extension
where K ≤ Z(C) ∩ C′ is a subgroup of the intersection of the center of C and the derived subgroup of C; this is more restrictive than central.
If the group G is finite and one considers only stem extensions, then there is a largest size for such a group C, and for every C of that size the subgroup K is isomorphic to the Schur multiplier of G. If the finite group G is moreover perfect
, then C is unique up to isomorphism and is itself perfect. Such C are often called universal perfect central extensions of G, or covering group (as it is a discrete analog of the universal covering space in topology). If the finite group G is not perfect, then its Schur covering groups (all such C of maximal order) are only isoclinic.
It is also called more briefly a universal central extension, but note that there is no largest central extension, as the direct product
of G and an abelian group
form a central extension of G of arbitrary size.
Stem extensions have the nice property that any lift of a generating set of G is a generating set of C. If the group G is presented
in terms of a free group
F on a set of generators, and a normal subgroup
R generated by a set of relations on the generators, so that G ≅ F/R, then the covering group itself can be presented in terms of F but with a smaller normal subgroup S, C ≅ F/S. Since the relations of G specify elements of K when considered as part of C, one must have S ≤ [F,R].
In fact if G is perfect, this is all that is needed: C ≅ [F,F]/[F,R] and M(G) ≅ K ≅ R/[F,R]. Because of this simplicity, expositions such as handle the perfect case first. The general case for the Schur multiplier is similar but ensures the extension is a stem extension by restricting to the derived subgroup of F: M(G) ≅ (R ∩ [F, F])/[F, R]. These are all slightly later results of Schur, who also gave a number of useful criteria for calculating them more explicitly.
, a group often originates from a presentation
. One important theme in this area of mathematics is to study presentations with as few relations as possible, such as one relator groups like Baumslag-Solitar groups. These groups are infinite groups with two generators and one relation, and an old result of Schreier shows that in any presentation with more generators than relations, the resulting group is infinite. The borderline case is thus quite interesting: finite groups with the same number of generators as relations are said to have an efficient presentation. For a group to have an efficient presentation, the group must have a trivial Schur multiplier because the minimum number of generators of the Schur multiplier is always less than or equal to the difference between the number of relations and the number of generators.
A fairly recent topic of research is to find efficient presentations for all finite simple groups with trivial Schur multipliers. Such presentations are in some sense nice because they are usually short, but they are difficult to find and to work with because they are ill-suited to standard methods such as coset enumeration.
, groups can often be described as finitely presented
groups and a fundamental question is to calculate their integral homology
. In particular, the second homology plays a special role and this led Hopf
to find an effective method for calculating it. The method in is also known as Hopf's integral homology formula and is identical to Schur's formula for the Schur multiplier of a finite, finitely presented group:
where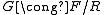
and F is a free group. The same formula also holds when G is a perfect group.
The recognition that these formulas were the same led Eilenberg
and Mac Lane
to the creation of cohomology of groups. In general,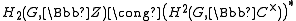
where the star denotes the algebraic dual group, and when G is finite, there is an unnatural
isomorphism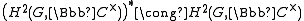
.
A perfect group
is one whose first integral homology vanishes. A superperfect group is one whose first two homology groups vanish. The Schur covers of finite perfect groups are superperfect. An acyclic group is a group all of whose reduced integral homology vanishes.
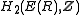
of the group E(R) of (infinite) elementary matrices with entries in R.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Schur multiplier or Schur multiplicator is the second homology group
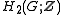of a group G.It was introduced by in his work on projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s.
Examples and properties
The Schur multiplier M(G) of a finite group G is a finite abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
whose exponent
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
divides the order of G. If a Sylow p-subgroup of G is cyclic for some p, then order of M(G) is not divisible by p.
In particular, if all Sylow p-subgroups of G are cyclic, then M(G) is trivial.
For instance, the Schur multiplier of the nonabelian group of order 6 is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
since every Sylow subgroup is cyclic. The Schur multiplier of the elementary abelian group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
of order 16 is an elementary abelian group of order 64, showing that the multiplier can be strictly larger than the group itself. The Schur multiplier of the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
is trivial, but the Schur multiplier of dihedral 2-groups
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
has order 2.
The Schur multipliers of the finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s are given at the list of finite simple groups. The covering groups of the alternating and symmetric groups
Covering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
are of considerable recent interest.
Relation to projective representations
Schur's original motivation for studying the multiplier was to classify projective representationProjective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of a group, and the modern formulation of his definition is the second cohomology group
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
H2(G,C×). A projective representation is much like a group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
except that instead of a homomorphism into the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,C), one takes a homomorphism into the projective general linear group PGL(n,C). In other words, a projective representation is a representation modulo the center.
showed that every finite group G has associated to it at least one finite group C, called a Schur cover, with the property that every projective representation of G can be lifted to an ordinary representation of C. The Schur cover is also known as a covering group or Darstellungsgruppe. The Schur covers of the finite simple groups are known, and each is an example of a quasisimple group
Quasisimple group
In mathematics, a quasisimple group is a group that is a perfect central extension E of a simple group S...
. The Schur cover of a perfect group
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
is uniquely determined up to isomorphism, but the Schur cover of a general finite group is only determined up to isoclinism.
Relation to central extensions
The study of such covering groups led naturally to the study of central and stem extensions.A central extension of a group G is an extension
- 1 → K → C → G → 1
where K ≤ Z(C) is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of C.
A stem extension of a group G is an extension
- 1 → K → C → G → 1
where K ≤ Z(C) ∩ C′ is a subgroup of the intersection of the center of C and the derived subgroup of C; this is more restrictive than central.
If the group G is finite and one considers only stem extensions, then there is a largest size for such a group C, and for every C of that size the subgroup K is isomorphic to the Schur multiplier of G. If the finite group G is moreover perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
, then C is unique up to isomorphism and is itself perfect. Such C are often called universal perfect central extensions of G, or covering group (as it is a discrete analog of the universal covering space in topology). If the finite group G is not perfect, then its Schur covering groups (all such C of maximal order) are only isoclinic.
It is also called more briefly a universal central extension, but note that there is no largest central extension, as the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of G and an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
form a central extension of G of arbitrary size.
Stem extensions have the nice property that any lift of a generating set of G is a generating set of C. If the group G is presented
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
in terms of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F on a set of generators, and a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
R generated by a set of relations on the generators, so that G ≅ F/R, then the covering group itself can be presented in terms of F but with a smaller normal subgroup S, C ≅ F/S. Since the relations of G specify elements of K when considered as part of C, one must have S ≤ [F,R].
In fact if G is perfect, this is all that is needed: C ≅ [F,F]/[F,R] and M(G) ≅ K ≅ R/[F,R]. Because of this simplicity, expositions such as handle the perfect case first. The general case for the Schur multiplier is similar but ensures the extension is a stem extension by restricting to the derived subgroup of F: M(G) ≅ (R ∩ [F, F])/[F, R]. These are all slightly later results of Schur, who also gave a number of useful criteria for calculating them more explicitly.
Relation to efficient presentations
In combinatorial group theoryCombinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
, a group often originates from a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
. One important theme in this area of mathematics is to study presentations with as few relations as possible, such as one relator groups like Baumslag-Solitar groups. These groups are infinite groups with two generators and one relation, and an old result of Schreier shows that in any presentation with more generators than relations, the resulting group is infinite. The borderline case is thus quite interesting: finite groups with the same number of generators as relations are said to have an efficient presentation. For a group to have an efficient presentation, the group must have a trivial Schur multiplier because the minimum number of generators of the Schur multiplier is always less than or equal to the difference between the number of relations and the number of generators.
A fairly recent topic of research is to find efficient presentations for all finite simple groups with trivial Schur multipliers. Such presentations are in some sense nice because they are usually short, but they are difficult to find and to work with because they are ill-suited to standard methods such as coset enumeration.
Relation to topology
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, groups can often be described as finitely presented
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
groups and a fundamental question is to calculate their integral homology
. In particular, the second homology plays a special role and this led HopfHeinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
to find an effective method for calculating it. The method in is also known as Hopf's integral homology formula and is identical to Schur's formula for the Schur multiplier of a finite, finitely presented group:
where
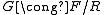and F is a free group. The same formula also holds when G is a perfect group.The recognition that these formulas were the same led Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
to the creation of cohomology of groups. In general,
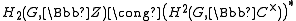where the star denotes the algebraic dual group, and when G is finite, there is an unnaturalNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
isomorphism
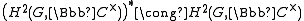.A perfect group
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
is one whose first integral homology vanishes. A superperfect group is one whose first two homology groups vanish. The Schur covers of finite perfect groups are superperfect. An acyclic group is a group all of whose reduced integral homology vanishes.
Applications
The second algebraic K-group K2(R) of a commutative ring R can be identified with the second homology group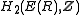of the group E(R) of (infinite) elementary matrices with entries in R.