Bianchi classification
Encyclopedia
In mathematics, the Bianchi classification, named for Luigi Bianchi
, is a classification of the 3-dimensional real Lie algebra
s into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes. (Sometimes two of the groups are included in the infinite families, giving 9 instead of 11 classes.) The term "Bianchi classification" is also used for similar classifications in other dimensions.
The classification of 3-dimensional complex Lie algebras is similar except that types VIII and IX become isomorphic, and types VI and VII both become part of a single family of Lie algebras.
The connected 3-dimensional Lie groups can be classified as follows: they are a quotient of the corresponding simply connected Lie group by a discrete subgroup of the center, so can be read off from the table above.
The groups are related to the 8 geometries of Thurston's geometrization conjecture
. More precisely, seven of the 8 geometries can be realized as a left-invariant metric on the simply connected group (sometimes in more than one way). The Thurston geometry of type S2×R cannot be realized in this way.
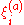which obey the following property:
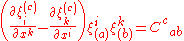
where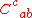
, the "structure constants" of the group, form a constant order-three tensor
antisymmetric in its lower two indices. For any three-dimensional Bianchi space,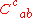
is given by the relationship
where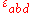
is the Levi-Civita symbol
,
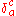is the Kronecker delta, and the vector 
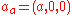and diagonal
tensor
are described by the following table, where 
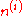gives the ith eigenvalue of 
; the parameter a runs over all positive real number
s:
, this classification is used for a homogeneous
spacetime
of dimension 3+1. The Friedmann-Lemaître-Robertson-Walker metrics are isotropic, which are particular cases of types I, V,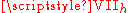
and IX. The Bianchi type I models include the Kasner metric
as a special case.
The Bianchi IX cosmologies include the Taub metric
. However, the dynamics near the singularity is approximately governed by a series of successive Kasner (Bianchi I) periods. The complicated dynamics,
which essentially amounts to billiard motion in a portion of hyperbolic space, exhibits chaotic behaviour, and is named Mixmaster
, and its analysis is referred to as the
BKL analysis
after Belinskii, Khalatnikov and Lifshitz.
More recent work has established a relation of (super-)gravity theories near a spacelike singularity (BKL-limit)
with Lorentzian Kac-Moody algebras, Weyl group
s and hyperbolic
Coxeter group
s.
Other more recent work is concerned with the discrete nature of the
Kasner map and a continuous generalisation.
into a product of the basis vectors associated with the space and a coordinate-independent tensor.
For a given metric
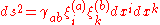(where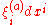 
are 1-forms
), the Ricci curvature tensor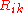
is given by:
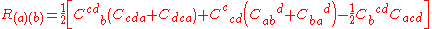
where the indices on the structure constants are raised and lowered with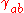
which is not a function of 
.
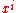Luigi Bianchi
- External links :* offers translations of some of Bianchi's papers, plus a biography of Bianchi.* PDF copy at * * * *...
, is a classification of the 3-dimensional real Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes. (Sometimes two of the groups are included in the infinite families, giving 9 instead of 11 classes.) The term "Bianchi classification" is also used for similar classifications in other dimensions.
Classification in dimension less than 3
- Dimension 0: The only Lie algebra is the abelian Lie algebra R0.
- Dimension 1: The only Lie algebra is the abelian Lie algebra R1, with outer automorphism group the group of non-zero real numbers.
- Dimension 2: There are two Lie algebras:
-
- (1) The abelian Lie algebra R2, with outer automorphism group GL2(R).
- (2) The solvable Lie algebra of 2×2 upper triangular matrices of trace 0. The simply connected group has trivial center and outer automorphism group of order 2.
Classification in dimension 3
All the 3-dimensional Lie algebras other than types VIII and IX can be constructed as a semidirect product of R2 and R, with R acting on R2 by some 2 by 2 matrix M. The different types correspond to different types of matrices M, as described below.- Type I: This is the abelian and unimodular Lie algebra R3. The simply connected group has center R3 and outer automorphism group GL3(R). This is the case when M is 0.
- Type II: Nilpotent and unimodular: Heisenberg algebra. The simply connected group has center R and outer automorphism group GL2(R). This is the case when M is nilpotent but not 0 (eigenvalues all 0).
- Type III: Solvable and not unimodular. This algebra is a product of R and the 2-dimensional non-abelian Lie algebra. (It is a limiting case of type VI, where one eigenvalue becomes zero.) The simply connected group has center R and outer automorphism group the group of non-zero real numbers. The matrix M has one zero and one non-zero eigenvalue.
- Type IV: Solvable and not unimodular. [y,z] = 0, [x,y] = y, [x, z] = y + z. The simply connected group has trivial center and outer automorphism group the product of the reals and a group of order 2. The matrix M has two equal non-zero eigenvalues, but is not semisimple.
- Type V: Solvable and not unimodular. [y,z] = 0, [x,y] = y, [x, z] = z. (A limiting case of type VI where both eigenvalues are equal.) The simply connected group has trivial center and outer automorphism group the elements of GL2(R) of determinant +1 or −1. The matrix M has two equal eigenvalues, and is semisimple.
- Type VI: Solvable and not unimodular. An infinite family. Semidirect products of R2 by R, where the matrix M has non-zero distinct real eigenvalues with non-zero sum. The simply connected group has trivial center and outer automorphism group a product of the non-zero real numbers and a group of order 2.
- Type VI0: Solvable and unimodular. This Lie algebra is the semidirect product of R2 by R, with R where the matrix M has non-zero distinct real eigenvalues with zero sum. It is the Lie algebra of the group of isometries of 2-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The simply connected group has trivial center and outer automorphism group the product of the positive real numbers with the dihedral group of order 8. - Type VII: Solvable and not unimodular. An infinite family. Semidirect products of R2 by R, where the matrix M has non-real and non-imaginary eigenvalues. The simply connected group has trivial center and outer automorphism group the non-zero reals.
- Type VII0: Solvable and unimodular. Semidirect products of R2 by R, where the matrix M has non-zero imaginary eigenvalues. This is the Lie algebra of the group of isometries of the plane. The simply connected group has center Z and outer automorphism group a product of the non-zero real numbers and a group of order 2.
- Type VIII: Semisimple and unimodular. The Lie algebra sl2(R) of traceless 2 by 2 matrices. The simply connected group has center Z and its outer automorphism group has order 2.
- Type IX: Semisimple and unimodular. The Lie algebra of the orthogonal group O3(R). The simply connected group has center of order 2 and trivial outer automorphism group, and is a spin group.
The classification of 3-dimensional complex Lie algebras is similar except that types VIII and IX become isomorphic, and types VI and VII both become part of a single family of Lie algebras.
The connected 3-dimensional Lie groups can be classified as follows: they are a quotient of the corresponding simply connected Lie group by a discrete subgroup of the center, so can be read off from the table above.
The groups are related to the 8 geometries of Thurston's geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
. More precisely, seven of the 8 geometries can be realized as a left-invariant metric on the simply connected group (sometimes in more than one way). The Thurston geometry of type S2×R cannot be realized in this way.
Structure constants
The three-dimensional Bianchi spaces each admit a set of three Killing vectors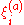 which obey the following property: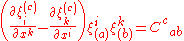where
, the "structure constants" of the group, form a constant order-three tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
antisymmetric in its lower two indices. For any three-dimensional Bianchi space,
is given by the relationshipwhere
is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
,
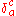is the Kronecker delta, and the vector 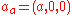and diagonalDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
tensor
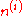are described by the following table, where gives the ith eigenvalue of ; the parameter a runs over all positive real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s:
| Bianchi type |  |
 |
 |
 |
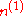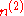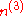notes |
|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 0 | describes Euclidean space Euclidean geometry Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these... |
| II | 0 | 1 | 0 | 0 | |
| III | 1 | 0 | 1 | -1 | the subcase of type VIa with  |
| IV | 1 | 0 | 0 | 1 | |
| V | 1 | 0 | 0 | 0 | has a hyper-pseudosphere Pseudosphere In geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid.... as a special case |
| VI0 | 0 | 1 | -1 | 0 | |
| VIa |  |
0 | 1 | -1 | when  , equivalent to type III |
| VII0 | 0 | 1 | 1 | 0 | has Euclidean space as a special case |
| VIIa |  |
0 | 1 | 1 | has a hyper-pseudosphere as a special case |
| VIII | 0 | 1 | 1 | -1 | |
| IX | 0 | 1 | 1 | 1 | has a hypersphere Hypersphere In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any... as a special case |
Cosmological application
In cosmologyCosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
, this classification is used for a homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
of dimension 3+1. The Friedmann-Lemaître-Robertson-Walker metrics are isotropic, which are particular cases of types I, V,
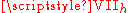and IX. The Bianchi type I models include the Kasner metricKasner metric
The Kasner metric is an exact solution to Einstein's theory of general relativity. It describes an anisotropic universe without matter...
as a special case.
The Bianchi IX cosmologies include the Taub metric
Taub-NUT vacuum
The Taub-NUT vacuum is an exact solution to Einstein's equations, a model universe formulated in the framework of general relativity that is homogeneous but anisotropic. It is based on a solution published by Abraham Haskel Taub in 1951....
. However, the dynamics near the singularity is approximately governed by a series of successive Kasner (Bianchi I) periods. The complicated dynamics,
which essentially amounts to billiard motion in a portion of hyperbolic space, exhibits chaotic behaviour, and is named Mixmaster
Mixmaster universe
The Mixmaster Universe is a solution to Einstein's field equations of general relativity studied by Charles Misner in an effort to better understand the dynamics of the early universe...
, and its analysis is referred to as the
BKL analysis
BKL singularity
A BKL singularity is a model of the dynamic evolution of the Universe near the initial singularity, described by an anisotropic, homogeneous, chaotic solution to Einstein's field equations of gravitation...
after Belinskii, Khalatnikov and Lifshitz.
More recent work has established a relation of (super-)gravity theories near a spacelike singularity (BKL-limit)
with Lorentzian Kac-Moody algebras, Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
s and hyperbolic
Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s.
Other more recent work is concerned with the discrete nature of the
Kasner map and a continuous generalisation.
Curvature of Bianchi spaces
The Bianchi spaces have the property that their Ricci tensors can be separatedSeparable differential equation
In mathematics, a separable differential equation may refer to one of two related things, both of which are differential equations that can be attacked by a method of separation of variables....
into a product of the basis vectors associated with the space and a coordinate-independent tensor.
For a given metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
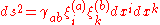(where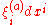 are 1-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
), the Ricci curvature tensor
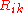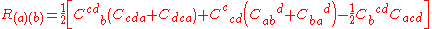
is given by:where the indices on the structure constants are raised and lowered with
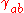which is not a function of .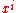