Mixmaster universe
Encyclopedia
The Mixmaster Universe is a solution to Einstein's field equations
of general relativity
studied by Charles Misner in an effort to better understand the dynamics of the early universe
. He hoped to solve the horizon problem
in a natural way by showing that the early universe underwent an oscillatory, chaotic
epoch.
three-sphere
s
. However, in the FRW universe, the 
can only expand or contract: the only dynamical parameter is overall size of the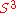 
, parameterized by the scale factor
. In the Mixmaster universe, the 
can expand or contract, but also distort anisotropically. Its evolution is described by a scale factor 
as well as by two shape parameters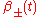 
. Values of the shape parameters describe distortions of the 
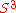that preserve its volume and also maintain a constant Ricci curvature
scalar. Therefore, as the three parameters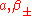
assume different values, homogeneity
but not isotropy
is preserved.
The model has a rich dynamical structure. Misner showed that the shape parameters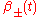
act like the coordinates of a point mass
moving in a triangular potential with steeply rising walls with friction. By studying the motion of this point, Misner showed that the physical universe would expand in some directions and contract in others, with the directions of expansion and contraction changing repeatedly. Because the potential is roughly triangular, Misner suggested that the evolution is chaotic.
where the
, considered as differential forms, are defined by
In terms of the coordinates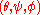
. These satisfy
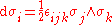
where
is the exterior derivative
and
the wedge product of differential forms. This relationship is reminiscent of the commutation relations for the lie algebra
of SU(2). The group manifold for SU(2) is the three-sphere
, and indeed the 
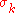describe the metric of an 
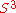that is allowed to distort anisotropically thanks to the presence of the 
.
Next Misner defines parameters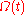
and 
which measure the volume of spatial slices, as well as "shape parameters"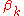 
, by
.
Since there is one condition on the three
, there should only be two free functions, which Misner chooses to be 
, defined as
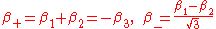
The evolution of the universe is then described by finding
as functions of 
.
horizon
in that direction is infinite, which he suggested meant that the horizon problem could be solved. Since the directions of expansion and contraction varied, presumably given enough time the horizon problem would get solved in every direction.
While an interesting example of gravitational chaos, it is widely recognized that the cosmological problems the Mixmaster universe attempts to solve are more elegantly tackled by cosmic inflation
. The metric Misner studied is also known as the Bianchi type
IX metric.
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
studied by Charles Misner in an effort to better understand the dynamics of the early universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
. He hoped to solve the horizon problem
Horizon problem
The horizon problem is a problem with the standard cosmological model of the Big Bang which was identified in the 1970s. It points out that different regions of the universe have not "contacted" each other because of the great distances between them, but nevertheless they have the same temperature...
in a natural way by showing that the early universe underwent an oscillatory, chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
epoch.
Discussion
The model is similar to the closed Friedmann-Lemaitre-Robertson-Walker universe, in that spatial slices are positively curved and are topologicallyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
three-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s
. However, in the FRW universe, the can only expand or contract: the only dynamical parameter is overall size of the 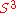, parameterized by the scale factorScale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
. In the Mixmaster universe, the can expand or contract, but also distort anisotropically. Its evolution is described by a scale factor as well as by two shape parameters 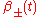. Values of the shape parameters describe distortions of the 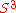that preserve its volume and also maintain a constant Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
scalar. Therefore, as the three parameters
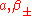assume different values, homogeneityHomogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
but not isotropy
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
is preserved.
The model has a rich dynamical structure. Misner showed that the shape parameters
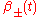act like the coordinates of a point massPoint particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
moving in a triangular potential with steeply rising walls with friction. By studying the motion of this point, Misner showed that the physical universe would expand in some directions and contract in others, with the directions of expansion and contraction changing repeatedly. Because the potential is roughly triangular, Misner suggested that the evolution is chaotic.
Metric
The metric studied by Misner (very slightly modified from his notation) is given by,where the
, considered as differential forms, are defined byIn terms of the coordinates
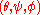. These satisfy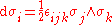where
is the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and
the wedge product of differential forms. This relationship is reminiscent of the commutation relations for the lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SU(2). The group manifold for SU(2) is the three-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
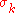, and indeed the describe the metric of an 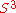that is allowed to distort anisotropically thanks to the presence of the .Next Misner defines parameters
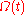and which measure the volume of spatial slices, as well as "shape parameters" 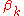, by.Since there is one condition on the three
, there should only be two free functions, which Misner chooses to be , defined as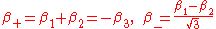The evolution of the universe is then described by finding
as functions of .Applications to Cosmology
Misner hoped that the chaos would churn up and smooth out the early universe. Also, during periods in which one direction was static (e.g., going from expansion to contraction) formally the HubbleHubble
Hubble is a surname and may refer to:* Brian Hubble , American painter and illustrator* Eddie Hubble , American Jazz trombonist* Edwin Hubble , American astronomer* Jack Hubble , English cricketer...
horizon
in that direction is infinite, which he suggested meant that the horizon problem could be solved. Since the directions of expansion and contraction varied, presumably given enough time the horizon problem would get solved in every direction.While an interesting example of gravitational chaos, it is widely recognized that the cosmological problems the Mixmaster universe attempts to solve are more elegantly tackled by cosmic inflation
Cosmic inflation
In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
. The metric Misner studied is also known as the Bianchi type
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
IX metric.