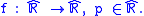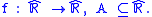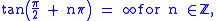Real projective line
Encyclopedia

Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the real projective line (also called the one-point compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, or the projectively extended real numbers), is the set
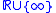 , also denoted by
, also denoted by  and by
and by  .
.The symbol
 represents the point at infinity, an idealized point that bridges the two "ends" of the real line.
represents the point at infinity, an idealized point that bridges the two "ends" of the real line.Dividing by zero
Unlike most mathematical models of the intuitive concept of 'number', this structure allows division by zeroDivision by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
:

for nonzero a. This structure, however, is not a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, and division does not retain its original algebraic meaning in it. The geometric interpretation is this: a vertical line has infinite slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
.
Extensions of the real line
The real projective line extends the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s in the same way that the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
extends the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, by adding a single point called conventionally
 .
.Compare the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
(also called the two-point compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of the real line), which does distinguish between
 and
and  .
.Order
The order relation cannot be extended to in a meaningful way. Given a real number a, there is no convincing reason to decide that
in a meaningful way. Given a real number a, there is no convincing reason to decide that  or that
or that  . Since
. Since  can't be compared with any of the other elements, there's no point in using this relation at all. As another example, both
can't be compared with any of the other elements, there's no point in using this relation at all. As another example, both  and
and  are true. However, order is used to make definitions in
are true. However, order is used to make definitions in 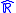 that are based on the properties of reals.
that are based on the properties of reals.Geometry
Fundamental to the idea that ∞ is a point no different from any other is the way the real projective line is a homogeneous spaceHomogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
, in fact homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. For example the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of 2×2 real invertible matrices has a transitive action on it. The group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
may be expressed by Möbius transformations, with the understanding that when the denominator of the linear fractional transformation is 0, the image is ∞.
The detailed analysis of the action shows that for any three distinct points P, Q and R, there is a linear fractional transformation taking P to 0, Q to 1, and R to ∞. This cannot be extended to 4-tuples of points, because the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
is invariant.
The terminology projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
is appropriate, because the points are in 1-1 correspondence with one-dimensional linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
s of R2.
Motivation for arithmetic operations
The arithmetic operations in this space are an extension of the same operations on reals. The motivation for the new definitions is the limits of functions of real numbers.Arithmetic operations which are defined

Arithmetic operations which are left undefined
The following cannot be motivated by considering limits of real functions, and any definition of them would require us to give up additional algebraic properties. Therefore, they are left undefined:
Algebraic properties
The following equalities mean: Either both sides are undefined, or both sides are defined and equal. This is true for any .
.
The following is true whenever the right-hand side is defined, for any
 .
.
In general, all laws of arithmetic are valid as long as all the occurring expressions are defined.
Intervals and topology
The concept of an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
can be extended to
 . However, since it is an unordered set, the interval has a slightly different meaning. The definitions for closed intervals are as follows (it is assumed that
. However, since it is an unordered set, the interval has a slightly different meaning. The definitions for closed intervals are as follows (it is assumed that ):
):
The corresponding open and half-open intervals are obtained by removing the endpoints.
 itself is also an interval, but cannot be represented with this bracket notation.
itself is also an interval, but cannot be represented with this bracket notation.The open intervals as base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
define a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on
 . Sufficient for a base are the finite open intervals and the intervals
. Sufficient for a base are the finite open intervals and the intervals  .
.As said, the topology is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. Thus it is metrizable corresponding (for a given homeomorphism) to the ordinary metric on this circle (either measured straight or along the circle). There is no metric which is an extension of the ordinary metric on R.
Interval arithmetic
Interval arithmeticInterval arithmetic
Interval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
is trickier in
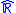 than in
than in  . However, the result of an arithmetic operation on intervals is always an interval. In particular, we have, for every
. However, the result of an arithmetic operation on intervals is always an interval. In particular, we have, for every 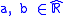 :
:
which is true even when the intervals involved include 0.
Calculus
The tools of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
can be used to analyze functions of
 . The definitions are motivated by the topology of this space.
. The definitions are motivated by the topology of this space.Neighbourhoods
Let .
.
- A is a neighbourhoodNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of x, if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
A contains an open interval B and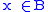 .
. - A is a right-sided neighbourhood of x, if and only if there is
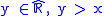 such that A contains
such that A contains 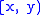 .
. - A is a left-sided neighbourhood of x, if and only if there is
 such that A contains
such that A contains 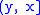 .
. - A is a (right-sided, left-sided) punctured neighbourhood of x, if and only if there is
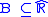 such that B is a (right-sided, left-sided) neighbourhood of x, and
such that B is a (right-sided, left-sided) neighbourhood of x, and  .
.
Basic definitions of limits
Let .
.The limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of f(x) as x approaches p is L, denoted

if and only if for every neighbourhood A of L, there is a punctured neighbourhood B of p, such that
 implies
implies  .
.The one-sided limit
One-sided limit
In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
of f(x) as x approaches p from the right (left) is L, denoted

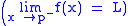
if and only if for every neighbourhood A of L, there is a right-sided (left-sided) punctured neighbourhood B of p, such that
 implies
implies 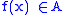 .
.It can be shown that
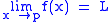 if and only if both
if and only if both 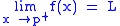 and
and  .
.Comparison with limits in 
The definitions given above can be compared with the usual definitions of limits of real functions. In the following statements,  , the first limit is as defined above, and the second limit is in the usual sense:
, the first limit is as defined above, and the second limit is in the usual sense:
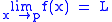 is equivalent to
is equivalent to 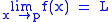 .
.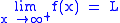 is equivalent to
is equivalent to 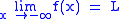 .
.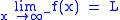 is equivalent to
is equivalent to 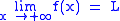 .
.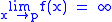 is equivalent to
is equivalent to 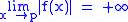 .
.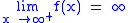 is equivalent to
is equivalent to  .
.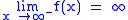 is equivalent to
is equivalent to 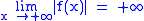 .
.
Extended definition of limits
Let . Then p is a limit point
. Then p is a limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of A if and only if every neighbourhood of p includes a point
 such that
such that  .
.Let
 , p a limit point of A. The limit of f(x) as x approaches p through A is L, if and only if for every neighbourhood B of L, there is a punctured neighbourhood C of p, such that
, p a limit point of A. The limit of f(x) as x approaches p through A is L, if and only if for every neighbourhood B of L, there is a punctured neighbourhood C of p, such that  implies
implies  .
.This corresponds to the regular topological definition of continuity, applied to the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
on
 , and the restriction of f to
, and the restriction of f to 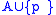 .
.Continuity
Letf is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
at p if and only if f is defined at p and:

Let
f is continuous in A if and only if for every
 , f is defined at p and the limit of f(x) as x approaches p through A is f(p).
, f is defined at p and the limit of f(x) as x approaches p through A is f(p).An interesting feature is that every rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
P(x)/Q(x), where P(x) and Q(x) have no common factor, is continuous in
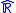 . Also, If tan is extended so that
. Also, If tan is extended so thatthen tan is continuous in
 . However, many elementary function
. However, many elementary functionElementary function (differential algebra)
In mathematics, an elementary function is a function of one variable built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations...
s, such as trigonometric and exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
functions, are discontinuous at
 . For example, sin is continuous in
. For example, sin is continuous in  but discontinuous at
but discontinuous at  .
.Thus 1/x is continuous on
 but not on the affinely extended real number system R. Conversely, the function arctan can be extended continuously on R, but not on
but not on the affinely extended real number system R. Conversely, the function arctan can be extended continuously on R, but not on 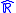 .
.