Squeeze mapping
Encyclopedia
In linear algebra
, a squeeze mapping is a type of linear map that preserves Euclidean area
of regions in the Cartesian plane, but is not a Euclidean motion.
For a fixed positive real number r, the mapping
→ (r x, y / r )
is the squeeze mapping with parameter r. Since
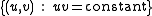
is a hyperbola
, if u = r x and v = y / r, then uv = xy and the points of the image of the squeeze mapping are on the same hyperbola as (x,y) is. For this reason it is natural to think of the squeeze mapping as a hyperbolic rotation, as did Émile Borel
in 1913, by analogy with circular rotations which preserves circles.
of their squeeze mappings is the squeeze mapping of their product. Therefore the collection of squeeze mappings forms a one-parameter group
isomorphic to the multiplicative group
of positive real numbers. An additive view of this group arises from consideration of hyperbolic sectors and hyperbolic angle
s. In fact, the invariant measure
of this group is hyperbolic angle.
From the point of view of the classical group
s, the group of squeeze mappings is SO+(1,1), the identity component
of the indefinite orthogonal group of 2 × 2 real matrices preserving the quadratic form
This is equivalent to preserving the form 
via the change of basis
and corresponds geometrically to preserving hyperbolae. The perspective of the group of squeeze mappings as hyperbolic rotation is analogous to interpreting the group SO(2) (the connected component of the definite orthogonal group
) preserving quadratic form
) as being circular rotations.
Note that the "SO+" notation corresponds to the fact that the reflections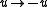
and 
are not allowed, though they preserve the form (in terms of x and y these are 
and 
); the additional "+" in the hyperbolic case (as compared with the circular case) is necessary to specify the identity component because the group O(1,1) has 4 connected components, while the group O(2) has 2 components: SO(1,1) has 2 components, while SO(2) only has 1. The fact that the squeeze transforms preserve area and orientation corresponds to the inclusion of subgroups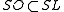 
– in this case SO(1,1) ⊂ SL(2) – of the subgroup of hyperbolic rotations in the special linear group
of transforms preserving area and orientation (a volume form
). In the language of Möbius transforms, the squeeze transformations are the hyperbolic elements in the classification of elements.
that the area under a hyperbola (concretely, the curve given by xy = k) is the same over [a,b] as over [c,d] when a/b = c/d – this corresponds to the area under a hyperbola being preserved under hyperbolic rotation, and was a key step in the development of the logarithm
. Formalization of the squeeze group required the theory of groups, which was not developed until the 19th century.
William Kingdon Clifford
was the author of Common Sense and the Exact Sciences, published in 1885. In the third chapter on Quantity he discusses area in three sections. Clifford uses the term "stretch" for magnification and the term "squeeze" for contraction. Taking a given square area as fundamental, Clifford relates other areas by stretch and squeeze. He develops this calculus to the point of illustrating the addition of fractions
in these terms in the second section. The third section is concerned with shear mapping as area-preserving.
The myth of Procrustes
is linked with this mapping in a 1967 educational (SMSG
) publication:
Attention had been drawn to this plane mapping by Modenov and Parkhomenko in their Russian book of 1961 which was translated in 1967 by Michael B. P. Slater. It included a diagram showing the squeezing of a circle into an ellipse.
Werner Greub of the University of Toronto
includes "pseudo-Euclidean rotation" in the chapter on symmetric bilinear functions of his text on linear algebra. This treatment in 1967 includes in short order both the diagonal form and the form with sinh and cosh.
The Mathematisch Centrum Amsterdam published E.R. Paërl's Representations of the Lorentz group and Projective Geometry in 1969. The squeeze mapping, written as a 2 × 2 diagonal matrix, Paërl calls a "hyperbolic screw".
In his 1999 monograph Classical Invariant Theory, Peter Olver discusses GL(2,R) and calls the group of squeeze mappings by the name the isobaric subgroup. However, in his 1986 book Applications of Lie Groups to Differential Equations (p. 127) he uses the term "hyperbolic rotation" for an equivalent mapping.
In 2004 the American Mathematical Society
published Transformation Groups for Beginners by S.V. Duzhin and B.D. Chebotarevsky which mentions hyperbolic rotation on page 225. There the parameter r is given as et and the transformation group of squeeze mappings is used to illustrate the invariance of a differential equation
under the group operation.
and a philosophical
application.
one of the fundamental motions of an incompressible flow
involves bifurcation of a flow running up against an immovable wall.
Representing the wall by the axis y = 0 and taking the parameter r = exp(t) where t is time, then the squeeze mapping with parameter r applied to an initial fluid state produces a flow with bifurcation left and right of the axis x = 0. The same model
gives fluid convergence when time is run backward. Indeed, the area
of any hyperbolic sector is invariant
under squeezing.
For another approach to a flow with hyperbolic streamlines
, see the article potential flow, section "Power law with n = 2".
In 1989 Ottino described the "linear isochoric two-dimensional flow" as
where K lies in the interval [−1,1]. The streamlines follow the curves
so negative K corresponds to an ellipse
and positive K to a hyperbola, with the rectangular case of the squeeze mapping corresponding to K = 1.
Stocker and Hosoi (2004) announced their approach to corner flow as follows:
Stocker and Hosoi then recall H.K. Moffatt's 1964 paper "Viscous and resistive eddies near a sharp corner" (Journal of Fluid Mechanics
18:1–18). Moffatt considers "flow in a corner between rigid boundaries, induced by an arbitrary disturbance at a large distance." According to Stocker and Hosoi,
multiplications and the "diagonal basis" which corresponds to the pair of light lines.
Formally, a squeeze preserves the hyperbolic metric expressed in the form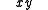
; in a different coordinate system. This application in the Theory of relativity
was noted in 1912 by Wilson and Lewis (see footnote p. 401 of reference),by Werner Greub in the 1960s, and in 1985 by Louis Kauffman
. Furthermore, Wolfgang Rindler
, in his popular textbook on relativity, used the squeeze mapping form of Lorentz transformations in his demonstration of their characteristic property (see equation 29.5 on page 45 of the 1969 edition, or equation 2.17 on page 37 of the 1977 edition, or equation 2.16 on page 52 of the 2001 edition).
and its inverse the exponential function
:
Definition: Sector(a,b) is the hyperbolic sector obtained with central rays to (a, 1/a) and (b, 1/b).
Lemma: If bc = ad, then there is a squeeze mapping that moves the sector(a,b) to sector(c,d).
Proof: Take parameter r = c/a so that (u,v) = (rx, y/r) takes (a, 1/a) to (c, 1/c) and (b, 1/b) to (d, 1/d).
Theorem (Gregoire de Saint-Vincent
1647) If bc = ad , then the quadrature of the hyperbola xy = 1 against the asymptote has equal areas between a and b compared to between c and d.
Proof: An argument adding and subtracting triangles of area ½, one triangle being {(0,0), (0,1), (1,1)}, shows the hyperbolic sector area is equal to the area along the asymptote. The theorem then follows from the lemma.
Theorem (Alphonse Antonio de Sarasa
1649) As area measured against the asymptote increases in arithmetic progression, the projections upon the asymptote increase in geometric sequence. Thus the areas form logarithms of the asymptote index.
For instance, for a standard position angle which runs from (1, 1) to (x, 1/x), one may ask "When is the hyperbolic angle equal to one?" The answer is the transcendental number
x = e (mathematical constant)
.
A squeeze with r = e moves the unit angle to one between (e, 1/e) and (ee, 1/ee) which subtends a sector also of area one. The geometric progression
corresponds to the asymptotic index achieved with each sum of areas
which is a proto-typical arithmetic progression
A + nd where A = 0 and d = 1 .
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a squeeze mapping is a type of linear map that preserves Euclidean area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of regions in the Cartesian plane, but is not a Euclidean motion.
For a fixed positive real number r, the mapping
→ (r x, y / r )
is the squeeze mapping with parameter r. Since
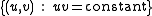
is a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, if u = r x and v = y / r, then uv = xy and the points of the image of the squeeze mapping are on the same hyperbola as (x,y) is. For this reason it is natural to think of the squeeze mapping as a hyperbolic rotation, as did Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
in 1913, by analogy with circular rotations which preserves circles.
Group theory
If r and s are positive real numbers, the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of their squeeze mappings is the squeeze mapping of their product. Therefore the collection of squeeze mappings forms a one-parameter group
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
isomorphic to the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of positive real numbers. An additive view of this group arises from consideration of hyperbolic sectors and hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
s. In fact, the invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
of this group is hyperbolic angle.
From the point of view of the classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s, the group of squeeze mappings is SO+(1,1), the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the indefinite orthogonal group of 2 × 2 real matrices preserving the quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
This is equivalent to preserving the form via the change of basisChange of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
and corresponds geometrically to preserving hyperbolae. The perspective of the group of squeeze mappings as hyperbolic rotation is analogous to interpreting the group SO(2) (the connected component of the definite orthogonal groupOrthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
) preserving quadratic form
) as being circular rotations.Note that the "SO+" notation corresponds to the fact that the reflections
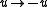and are not allowed, though they preserve the form (in terms of x and y these are and ); the additional "+" in the hyperbolic case (as compared with the circular case) is necessary to specify the identity component because the group O(1,1) has 4 connected components, while the group O(2) has 2 components: SO(1,1) has 2 components, while SO(2) only has 1. The fact that the squeeze transforms preserve area and orientation corresponds to the inclusion of subgroups 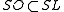– in this case SO(1,1) ⊂ SL(2) – of the subgroup of hyperbolic rotations in the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
of transforms preserving area and orientation (a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
). In the language of Möbius transforms, the squeeze transformations are the hyperbolic elements in the classification of elements.
Literature
Among the earliest recognition of a squeeze symmetry was the 1647 discovery by Grégoire de Saint-VincentGrégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
that the area under a hyperbola (concretely, the curve given by xy = k) is the same over [a,b] as over [c,d] when a/b = c/d – this corresponds to the area under a hyperbola being preserved under hyperbolic rotation, and was a key step in the development of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
. Formalization of the squeeze group required the theory of groups, which was not developed until the 19th century.
William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
was the author of Common Sense and the Exact Sciences, published in 1885. In the third chapter on Quantity he discusses area in three sections. Clifford uses the term "stretch" for magnification and the term "squeeze" for contraction. Taking a given square area as fundamental, Clifford relates other areas by stretch and squeeze. He develops this calculus to the point of illustrating the addition of fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
in these terms in the second section. The third section is concerned with shear mapping as area-preserving.
The myth of Procrustes
Procrustes
In Greek mythology Procrustes or "the stretcher [who hammers out the metal]", also known as Prokoptas or Damastes "subduer", was a rogue smith and bandit from Attica who physically attacked people by stretching them or cutting off their legs, so as to force them to fit the size of an iron bed...
is linked with this mapping in a 1967 educational (SMSG
School Mathematics Study Group
The School Mathematics Study Group was an American academic think tank focused on the subject of reform in mathematics education. Directed by Edward G...
) publication:
- Among the linear transformations, we have considered similarities, which preserve ratios of distances, but have not touched upon the more bizarre varieties, such as the Procrustean stretch (which changes a circle into an ellipse of the same area).
- Coxeter & Greitzer, pp. 100, 101.
Attention had been drawn to this plane mapping by Modenov and Parkhomenko in their Russian book of 1961 which was translated in 1967 by Michael B. P. Slater. It included a diagram showing the squeezing of a circle into an ellipse.
Werner Greub of the University of Toronto
University of Toronto
The University of Toronto is a public research university in Toronto, Ontario, Canada, situated on the grounds that surround Queen's Park. It was founded by royal charter in 1827 as King's College, the first institution of higher learning in Upper Canada...
includes "pseudo-Euclidean rotation" in the chapter on symmetric bilinear functions of his text on linear algebra. This treatment in 1967 includes in short order both the diagonal form and the form with sinh and cosh.
The Mathematisch Centrum Amsterdam published E.R. Paërl's Representations of the Lorentz group and Projective Geometry in 1969. The squeeze mapping, written as a 2 × 2 diagonal matrix, Paërl calls a "hyperbolic screw".
In his 1999 monograph Classical Invariant Theory, Peter Olver discusses GL(2,R) and calls the group of squeeze mappings by the name the isobaric subgroup. However, in his 1986 book Applications of Lie Groups to Differential Equations (p. 127) he uses the term "hyperbolic rotation" for an equivalent mapping.
In 2004 the American Mathematical Society
American Mathematical Society
The American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
published Transformation Groups for Beginners by S.V. Duzhin and B.D. Chebotarevsky which mentions hyperbolic rotation on page 225. There the parameter r is given as et and the transformation group of squeeze mappings is used to illustrate the invariance of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
under the group operation.
Applications
In studying linear algebra there are the purely abstract applications such as illustration of the singular-value decomposition or in the important role of the squeeze mapping in the structure of 2 × 2 real matrices. These applications are somewhat bland compared to two physicalPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and a philosophical
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
application.
Corner flow
In fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
one of the fundamental motions of an incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
involves bifurcation of a flow running up against an immovable wall.
Representing the wall by the axis y = 0 and taking the parameter r = exp(t) where t is time, then the squeeze mapping with parameter r applied to an initial fluid state produces a flow with bifurcation left and right of the axis x = 0. The same model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
gives fluid convergence when time is run backward. Indeed, the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of any hyperbolic sector is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under squeezing.
For another approach to a flow with hyperbolic streamlines
Streamlines, streaklines and pathlines
Fluid flow is characterized by a velocity vector field in three-dimensional space, within the framework of continuum mechanics. Streamlines, streaklines and pathlines are field lines resulting from this vector field description of the flow...
, see the article potential flow, section "Power law with n = 2".
In 1989 Ottino described the "linear isochoric two-dimensional flow" as
where K lies in the interval [−1,1]. The streamlines follow the curves
so negative K corresponds to an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
and positive K to a hyperbola, with the rectangular case of the squeeze mapping corresponding to K = 1.
Stocker and Hosoi (2004) announced their approach to corner flow as follows:
- we suggest an alternative formulation to account for the corner-like geometry, based on the use of hyperbolic coordinates, which allows substantial analytical progress towards determination of the flow in a Plateau border and attached liquid threads. We consider a region of flow forming an angle of π/2 and delimited on the left and bottom by symmetry planes.
Stocker and Hosoi then recall H.K. Moffatt's 1964 paper "Viscous and resistive eddies near a sharp corner" (Journal of Fluid Mechanics
Journal of Fluid Mechanics
The Journal of Fluid Mechanics is the leading scientific journal in the field of fluid mechanics. It publishes original work on theoretical, computational and experimental aspects of the subject. The journal is usually referred to by its initials JFM by academics in the field. Within citations,...
18:1–18). Moffatt considers "flow in a corner between rigid boundaries, induced by an arbitrary disturbance at a large distance." According to Stocker and Hosoi,
- For a free fluid in a square corner, Moffatt's (antisymmetric) stream function ... [indicates] that hyperbolic coordinates are indeed the natural choice to describe these flows.
Relativistic spacetime
Select (0,0) for a "here and now" in a spacetime. Light radiant left and right through this central event tracks two lines in the spacetime, lines that can be used to give coordinates to events away from (0,0). Trajectories of lesser velocity track closer to the original timeline (0,t). Any such velocity can be viewed as a zero velocity under a squeeze mapping called a Lorentz boost. This insight follows from a study of split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
multiplications and the "diagonal basis" which corresponds to the pair of light lines.
Formally, a squeeze preserves the hyperbolic metric expressed in the form
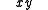; in a different coordinate system. This application in the Theory of relativityTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
was noted in 1912 by Wilson and Lewis (see footnote p. 401 of reference),by Werner Greub in the 1960s, and in 1985 by Louis Kauffman
Louis Kauffman
Louis H. Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago...
. Furthermore, Wolfgang Rindler
Wolfgang Rindler
Wolfgang Rindler is a leading physicist working in the field of General Relativity where he is well known for introducing the term "event horizon", Rindler coordinates, and for popularizing the use of spinors in general relativity. He is also a prolific textbook author.-Education:Rindler gained...
, in his popular textbook on relativity, used the squeeze mapping form of Lorentz transformations in his demonstration of their characteristic property (see equation 29.5 on page 45 of the 1969 edition, or equation 2.17 on page 37 of the 1977 edition, or equation 2.16 on page 52 of the 2001 edition).
Bridge to transcendentals
The area-preserving property of squeeze mapping has an application in setting the foundation of the transcendental functions natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
and its inverse the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
:
Definition: Sector(a,b) is the hyperbolic sector obtained with central rays to (a, 1/a) and (b, 1/b).
Lemma: If bc = ad, then there is a squeeze mapping that moves the sector(a,b) to sector(c,d).
Proof: Take parameter r = c/a so that (u,v) = (rx, y/r) takes (a, 1/a) to (c, 1/c) and (b, 1/b) to (d, 1/d).
Theorem (Gregoire de Saint-Vincent
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
1647) If bc = ad , then the quadrature of the hyperbola xy = 1 against the asymptote has equal areas between a and b compared to between c and d.
Proof: An argument adding and subtracting triangles of area ½, one triangle being {(0,0), (0,1), (1,1)}, shows the hyperbolic sector area is equal to the area along the asymptote. The theorem then follows from the lemma.
Theorem (Alphonse Antonio de Sarasa
Alphonse Antonio de Sarasa
Alphonse Antonio de Sarasa was a Jesuit mathematician who contributed to the understanding of logarithms, particularly as areas under a hyperbola....
1649) As area measured against the asymptote increases in arithmetic progression, the projections upon the asymptote increase in geometric sequence. Thus the areas form logarithms of the asymptote index.
For instance, for a standard position angle which runs from (1, 1) to (x, 1/x), one may ask "When is the hyperbolic angle equal to one?" The answer is the transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
x = e (mathematical constant)
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
.
A squeeze with r = e moves the unit angle to one between (e, 1/e) and (ee, 1/ee) which subtends a sector also of area one. The geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
- e, e2, e3, ..., en, ...
corresponds to the asymptotic index achieved with each sum of areas
- 1,2,3, ..., n,...
which is a proto-typical arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
A + nd where A = 0 and d = 1 .
See also
- Equi-areal mapping
- Indefinite orthogonal group
- Isochoric processIsochoric processAn isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant...
- Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...