Streamlines, streaklines and pathlines
Encyclopedia
Fluid flow is characterized by a velocity
vector field
in three-dimensional space
, within the framework of continuum mechanics
. Streamlines, streaklines and pathlines are field line
s resulting from this vector field description of the flow. They differ only when the flow changes with time: that is, when the flow is not steady.
By definition, different streamlines at the same instant in a flow do not intersect, because a fluid particle cannot have two different velocities at the same point. Similarly, streaklines cannot intersect themselves or other streaklines, because two particles cannot be present at the same location at the same instant of time; unless the origin point of one of the streaklines also belongs to the streakline of the other origin point. However, pathlines are allowed to intersect themselves or other pathlines (except the starting and end points of the different pathlines, which need to be distinct).
Streamlines and timelines provide a snapshot of some flowfield characteristics, whereas streaklines and pathlines depend on the full time-history of the flow. However, often sequences of timelines (and streaklines) at different instants—being presented either in a single image or with a video stream—may be used to provide insight in the flow and its history.
If a line, curve or closed curve is used as start point for a continuous set of streamlines, the result is a stream surface. In the case of a closed curve in a steady flow, fluid that is inside a stream surface must remain forever within that same stream surface, because the streamlines are tangent to the flow velocity. A scalar function whose contour line
s define the streamlines is known as the stream function
.
Dye line may refer either to a streakline: dye released gradually from a fixed location during time; or it may refer to a timeline: a line of dye applied instantaneously at a certain moment in time, and observed at a later instant.
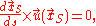
with "×" denoting the vector cross product
and
is the parametric representation
of just one streamline at one moment in time.
If the components of the velocity are written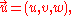
and those of the streamline as 
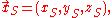we deduce:
which shows that the curves are parallel to the velocity vector. Here
is a variable
which parametrizes
the curve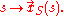
Streamlines are calculated instantaneously, meaning that at one instance of time they are calculated throughout the fluid from the instantaneous flow velocity
field
.
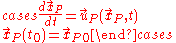
The suffix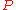
indicates that we are following the motion of a fluid particle.
Note that at point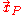
the curve is parallel to the flow velocity vector 
, where the velocity vector is evaluated at the position of the particle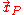 
at that time 
.
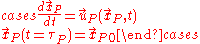
where,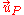
is the velocity of a particle 
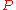at location 
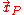and time 
. The parameter 
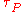, parametrizes the streakline 
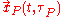and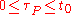 
, where 
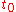is a time of interest.
, further on that streamline the equations governing the flow will send it in a certain direction 
. As the equations that govern the flow remain the same when another particle reaches 
it will also go in the direction 
. If the flow is not steady then when the next particle reaches position 
the flow would have changed and the particle will go in a different direction.
This is useful, because it is usually very difficult to look at streamlines in an experiment. However, if the flow is steady, one can use streaklines to describe the streamline pattern.
are different from those observed in another inertial reference frame. For instance, the streamlines in the air
around an aircraft
wing
are defined differently for the passengers in the aircraft than for an observer
on the ground. When possible, fluid dynamicists try to find a reference frame in which the flow is steady, so that they can use experimental methods of creating streaklines to identify the streamlines. In the aircraft example, the observer on the ground will observe unsteady flow, and the observers in the aircraft will observe steady flow, with constant streamlines.
, which describes the relationship between pressure and velocity in an inviscid fluid, is derived for locations along a streamline.
The curvature of a streamline is related to the pressure
gradient acting perpendicular to the streamline. The center of curvature of the streamline lies in the direction of decreasing radial pressure. The magnitude of the radial pressure gradient can be calculated directly from the density of the fluid, the curvature of the streamline and the local velocity.
Engineers
often use dye
s in water or smoke
in air in order to see streaklines, from which pathlines can be calculated. Streaklines are identical to streamlines for steady flow. Further, dye can be used to create timelines. The patterns guide their design modifications, aiming to reduce the drag. This task is known as streamlining, and the resulting design is referred to as being streamlined. Streamlined objects and organisms, like steam locomotives, streamliner
s, cars
and dolphin
s are often aesthetically pleasing to the eye. The Streamline Moderne
style, an 1930s and 1940s offshoot of Art Deco
, brought flowing lines to architecture and design of the era. The canonical example of a streamlined shape is a chicken egg
with the blunt end facing forwards. This shows clearly that the curvature of the front surface can be much steeper than the back of the object. Most drag is caused by eddies in the fluid behind the moving object, and the objective should be to allow the fluid to slow down after passing around the object, and regain pressure, without forming eddies.
The same terms have since become common vernacular to describe any process that smooths an operation. For instance, it is common to hear references to streamlining a business practice, or operation.
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
, within the framework of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
. Streamlines, streaklines and pathlines are field line
Field line
A field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
s resulting from this vector field description of the flow. They differ only when the flow changes with time: that is, when the flow is not steady.
- Streamlines are a family of curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s that are instantaneously tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
vector of the flow. These show the direction a fluid element will travel in at any point in time.
- Streaklines are the locusLocus (mathematics)In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points of all the fluid particles that have passed continuously through a particular spatial point in the past. Dye steadily injected into the fluid at a fixed point extends along a streakline.
- Pathlines are the trajectoriesTrajectoryA trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
that individual fluid particles follow. These can be thought of as a "recording" of the path a fluid element in the flow takes over a certain period. The direction the path takes will be determined by the streamlines of the fluid at each moment in time.
- Timelines are the lines formed by a set of fluid particles that were marked at a previous instant in time, creating a line or a curve that is displaced in time as the particles move.
By definition, different streamlines at the same instant in a flow do not intersect, because a fluid particle cannot have two different velocities at the same point. Similarly, streaklines cannot intersect themselves or other streaklines, because two particles cannot be present at the same location at the same instant of time; unless the origin point of one of the streaklines also belongs to the streakline of the other origin point. However, pathlines are allowed to intersect themselves or other pathlines (except the starting and end points of the different pathlines, which need to be distinct).
Streamlines and timelines provide a snapshot of some flowfield characteristics, whereas streaklines and pathlines depend on the full time-history of the flow. However, often sequences of timelines (and streaklines) at different instants—being presented either in a single image or with a video stream—may be used to provide insight in the flow and its history.
If a line, curve or closed curve is used as start point for a continuous set of streamlines, the result is a stream surface. In the case of a closed curve in a steady flow, fluid that is inside a stream surface must remain forever within that same stream surface, because the streamlines are tangent to the flow velocity. A scalar function whose contour line
Contour line
A contour line of a function of two variables is a curve along which the function has a constant value. In cartography, a contour line joins points of equal elevation above a given level, such as mean sea level...
s define the streamlines is known as the stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
.
Dye line may refer either to a streakline: dye released gradually from a fixed location during time; or it may refer to a timeline: a line of dye applied instantaneously at a certain moment in time, and observed at a later instant.
Streamlines
Streamlines are defined as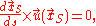with "×" denoting the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and
is the parametric representationParametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of just one streamline at one moment in time.
If the components of the velocity are written
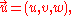and those of the streamline as 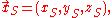we deduce:which shows that the curves are parallel to the velocity vector. Here
is a variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
which parametrizes
Parametrization
Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....
the curve
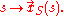Streamlines are calculated instantaneously, meaning that at one instance of time they are calculated throughout the fluid from the instantaneous flow velocityFlow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
.
Pathlines
Pathlines are defined by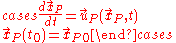The suffix
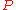indicates that we are following the motion of a fluid particle.Note that at point
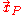the curve is parallel to the flow velocity vector , where the velocity vector is evaluated at the position of the particle 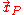at that time .Streaklines
Streaklines can be expressed as,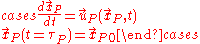where,
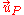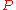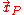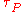is the velocity of a particle at location and time . The parameter , parametrizes the streakline 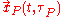and 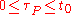, where 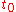is a time of interest.Steady flows
In steady flow (when the velocity vector-field does not change with time), the streamlines, pathlines, and streaklines coincide. This is because when a particle on a streamline reaches a point,, further on that streamline the equations governing the flow will send it in a certain direction . As the equations that govern the flow remain the same when another particle reaches it will also go in the direction . If the flow is not steady then when the next particle reaches position the flow would have changed and the particle will go in a different direction.This is useful, because it is usually very difficult to look at streamlines in an experiment. However, if the flow is steady, one can use streaklines to describe the streamline pattern.
Frame dependence
Streamlines are frame-dependent. That is, the streamlines observed in one inertial reference frameInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
are different from those observed in another inertial reference frame. For instance, the streamlines in the air
Earth's atmosphere
The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
around an aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
wing
Wing
A wing is an appendage with a surface that produces lift for flight or propulsion through the atmosphere, or through another gaseous or liquid fluid...
are defined differently for the passengers in the aircraft than for an observer
Observation
Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
on the ground. When possible, fluid dynamicists try to find a reference frame in which the flow is steady, so that they can use experimental methods of creating streaklines to identify the streamlines. In the aircraft example, the observer on the ground will observe unsteady flow, and the observers in the aircraft will observe steady flow, with constant streamlines.
Applications
Knowledge of the streamlines can be useful in fluid dynamics. For example, Bernoulli's principleBernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
, which describes the relationship between pressure and velocity in an inviscid fluid, is derived for locations along a streamline.
The curvature of a streamline is related to the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
gradient acting perpendicular to the streamline. The center of curvature of the streamline lies in the direction of decreasing radial pressure. The magnitude of the radial pressure gradient can be calculated directly from the density of the fluid, the curvature of the streamline and the local velocity.
Engineers
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
often use dye
Dye
A dye is a colored substance that has an affinity to the substrate to which it is being applied. The dye is generally applied in an aqueous solution, and requires a mordant to improve the fastness of the dye on the fiber....
s in water or smoke
Smoke
Smoke is a collection of airborne solid and liquid particulates and gases emitted when a material undergoes combustion or pyrolysis, together with the quantity of air that is entrained or otherwise mixed into the mass. It is commonly an unwanted by-product of fires , but may also be used for pest...
in air in order to see streaklines, from which pathlines can be calculated. Streaklines are identical to streamlines for steady flow. Further, dye can be used to create timelines. The patterns guide their design modifications, aiming to reduce the drag. This task is known as streamlining, and the resulting design is referred to as being streamlined. Streamlined objects and organisms, like steam locomotives, streamliner
Streamliner
A streamliner is a vehicle incorporating streamlining in a shape providing reduced air resistance. The term is applied to high-speed railway trainsets of the 1930s to 1950s, and to their successor "bullet trains". Less commonly, the term is applied to fully faired recumbent bicycles...
s, cars
Automobile
An automobile, autocar, motor car or car is a wheeled motor vehicle used for transporting passengers, which also carries its own engine or motor...
and dolphin
Dolphin
Dolphins are marine mammals that are closely related to whales and porpoises. There are almost forty species of dolphin in 17 genera. They vary in size from and , up to and . They are found worldwide, mostly in the shallower seas of the continental shelves, and are carnivores, mostly eating...
s are often aesthetically pleasing to the eye. The Streamline Moderne
Streamline Moderne
Streamline Moderne, sometimes referred to by either name alone or as Art Moderne, was a late type of the Art Deco design style which emerged during the 1930s...
style, an 1930s and 1940s offshoot of Art Deco
Art Deco
Art deco , or deco, is an eclectic artistic and design style that began in Paris in the 1920s and flourished internationally throughout the 1930s, into the World War II era. The style influenced all areas of design, including architecture and interior design, industrial design, fashion and...
, brought flowing lines to architecture and design of the era. The canonical example of a streamlined shape is a chicken egg
Oval (geometry)
In technical drawing, an oval is a figure constructed from two pairs of arcs, with two different radii . The arcs are joined at a point, in which lines tangential to both joining arcs lie on the same line, thus making the joint smooth...
with the blunt end facing forwards. This shows clearly that the curvature of the front surface can be much steeper than the back of the object. Most drag is caused by eddies in the fluid behind the moving object, and the objective should be to allow the fluid to slow down after passing around the object, and regain pressure, without forming eddies.
The same terms have since become common vernacular to describe any process that smooths an operation. For instance, it is common to hear references to streamlining a business practice, or operation.
See also
- Drag coefficientDrag coefficientIn fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
- Equipotential surfaceEquipotential surfaceEquipotential surfaces are surfaces of constant scalar potential. They are used to visualize an -dimensional scalar potential function in dimensional space...
- Flow visualizationFlow visualizationFlow visualization in fluid dynamics is used to make the flow patterns visible, in order to get a qualitative or quantitative information on them.- Overview :...
- Potential flow around a circular cylinderPotential flow around a circular cylinderIn mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity...
- Stream functionStream functionThe stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
- StreamsurfaceStreamsurfaceIn Scientific Visualization a Streamsurface is the 3D generalization of a streamline. It is the union of all streamlines seeded densely on a curve. Like a streamline, a streamsurface is used to to visualize flows - three-dimensional flows in this case....