
Potential flow around a circular cylinder
Encyclopedia
In mathematics
, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow
. Unlike a real fluid, this solution indicates a net zero drag
on the body, a result known as d'Alembert's paradox
.
"The flow of an incompressible fluid past a cylinder is one of the first mathematical models that a student of fluid dynamics encounters. This flow is an excellent vehicle for the study of concepts that will be encountered numerous times in mathematical physics, such as vector fields, coordinate transformations, and most important, the physical interpretation of mathematical results."
 is placed in two-dimensional, incompressible, inviscid flow.
is placed in two-dimensional, incompressible, inviscid flow.
The goal is to find the steady velocity vector and pressure
and pressure
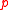 in a plane, subject to the condition that far from the cylinder the velocity vector is
in a plane, subject to the condition that far from the cylinder the velocity vector is

where is a constant, and at the boundary of the cylinder
is a constant, and at the boundary of the cylinder
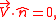
where is the vector normal
is the vector normal
to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density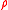 . The flow therefore remains without vorticity, or is said to be irrotational, with
. The flow therefore remains without vorticity, or is said to be irrotational, with
 everywhere. Being irrotational, there must exist a velocity potential
everywhere. Being irrotational, there must exist a velocity potential  :
:

Being incompressible,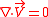 , so
, so  must satisfy Laplace's equation
must satisfy Laplace's equation
:

The solution for is obtained most easily in polar coordinates
is obtained most easily in polar coordinates  and
and  , related to conventional Cartesian coordinates by
, related to conventional Cartesian coordinates by 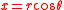 and
and  . In polar coordinates, Laplace's equation is:
. In polar coordinates, Laplace's equation is:
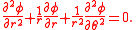
The solution that satisfies the boundary conditions is

The velocity components in polar coordinates are obtained from the components of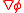 in polar coordinates:
in polar coordinates:
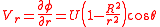
and

Being invisicid and irrotational, Bernoulli's equation allows the solution for pressure field to be obtained directly form the velocity field:
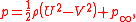
where the constants and
and  appear so that
appear so that 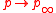 far from the cylinder, where
far from the cylinder, where  .
.
Using
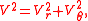

In the figures, the colorized field referred to as "pressure" is a plot of
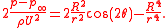
On the surface of the cylinder, or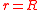 , pressure varies from a maximum of 1 (red color) at the stagnation points at
, pressure varies from a maximum of 1 (red color) at the stagnation points at  and
and
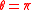 to a minimum of -3 (purple) on the sides of the cylinder, at
to a minimum of -3 (purple) on the sides of the cylinder, at 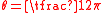 and
and  Likewise,
Likewise, 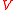 varies from V=0 at the stagnation points to
varies from V=0 at the stagnation points to  on the sides, in the low pressure.
on the sides, in the low pressure.
can be found such that

It follows from this definition, using vector identities,
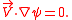
Therefore a contour of a constant value of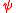 will also be a stream line, a line tangent to
will also be a stream line, a line tangent to 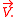 For the flow past a cylinder, we find:
For the flow past a cylinder, we find:
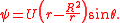
is linear, and is one of the most elementary partial differential equation
s. This simple equation yields the entire solution for both and
and 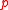 because of the constraint of irrotationality and incompressibility. Having obtained the solution for
because of the constraint of irrotationality and incompressibility. Having obtained the solution for  and
and 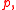 the consistency of the pressure gradient with the accelerations can be noted.
the consistency of the pressure gradient with the accelerations can be noted.
The dynamic pressure at the upstream stagnation point has value of a value needed to decelerate the free stream flow of speed
a value needed to decelerate the free stream flow of speed 
This same value appears at the downstream stagnation point, this high pressure is again need to decelerate the flow to zero speed. This symmetry arises only because the flow is completely frictionless.
The low pressure on sides on the cylinder is needed to provide the centripetal acceleration of the flow:
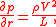
where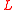 is the radius of curvature of the flow. But
is the radius of curvature of the flow. But 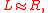 and
and  The integral of the equation for centripetal acceleration, which will over a distance
The integral of the equation for centripetal acceleration, which will over a distance  will thus yield
will thus yield
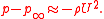
The exact solution has, for the lowest pressure,
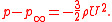
The low pressure, which must be present to provide the centripetal acceleration, will also increase the flow speed as the fluid travels from higher to lower values of pressure. Thus we find the maximum speed in the flow,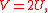 in the low pressure on the sides of the cylinder.
in the low pressure on the sides of the cylinder.
A value of is consistent with conservation of the volume of fluid. With the cylinder blocking some of the flow,
is consistent with conservation of the volume of fluid. With the cylinder blocking some of the flow, 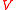 must be greater than
must be greater than  somewhere in the plane through the center of the cylinder and transverse to the flow.
somewhere in the plane through the center of the cylinder and transverse to the flow.
on the cylinder, a property known as d'Alembert's paradox
.
Unlike an ideal inviscid fluid, a viscous flow past a cylinder, no matter how small the viscosity, will acquire vorticity in a thin boundary layer
adjacent to the cylinder. Boundary layer separation can occur, and a trailing wake
will occur behind the cylinder. The pressure will be lower on the wake side of the cylinder, than on the upstream side, resulting in a drag force in the downstream direction.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
. Unlike a real fluid, this solution indicates a net zero drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
on the body, a result known as d'Alembert's paradox
D'Alembert's paradox
In fluid dynamics, d'Alembert's paradox is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert. D'Alembert proved that – for incompressible and inviscid potential flow – the drag force is zero on a body moving with constant velocity relative to the fluid...
.
"The flow of an incompressible fluid past a cylinder is one of the first mathematical models that a student of fluid dynamics encounters. This flow is an excellent vehicle for the study of concepts that will be encountered numerous times in mathematical physics, such as vector fields, coordinate transformations, and most important, the physical interpretation of mathematical results."
Mathematical solution
A cylinder (or disk) of radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
 is placed in two-dimensional, incompressible, inviscid flow.
is placed in two-dimensional, incompressible, inviscid flow.The goal is to find the steady velocity vector
 and pressure
and pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
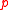 in a plane, subject to the condition that far from the cylinder the velocity vector is
in a plane, subject to the condition that far from the cylinder the velocity vector is
where
 is a constant, and at the boundary of the cylinder
is a constant, and at the boundary of the cylinder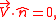
where
 is the vector normal
is the vector normalSurface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density
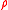 . The flow therefore remains without vorticity, or is said to be irrotational, with
. The flow therefore remains without vorticity, or is said to be irrotational, with everywhere. Being irrotational, there must exist a velocity potential
everywhere. Being irrotational, there must exist a velocity potential  :
:
Being incompressible,
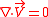 , so
, so  must satisfy Laplace's equation
must satisfy Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:

The solution for
 is obtained most easily in polar coordinates
is obtained most easily in polar coordinates  and
and  , related to conventional Cartesian coordinates by
, related to conventional Cartesian coordinates by 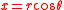 and
and  . In polar coordinates, Laplace's equation is:
. In polar coordinates, Laplace's equation is: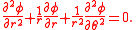
The solution that satisfies the boundary conditions is

The velocity components in polar coordinates are obtained from the components of
 in polar coordinates:
in polar coordinates: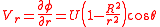
and

Being invisicid and irrotational, Bernoulli's equation allows the solution for pressure field to be obtained directly form the velocity field:
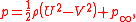
where the constants
 and
and  appear so that
appear so that 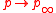 far from the cylinder, where
far from the cylinder, where  .
.Using
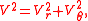

In the figures, the colorized field referred to as "pressure" is a plot of
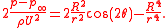
On the surface of the cylinder, or
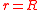 , pressure varies from a maximum of 1 (red color) at the stagnation points at
, pressure varies from a maximum of 1 (red color) at the stagnation points at  and
and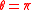 to a minimum of -3 (purple) on the sides of the cylinder, at
to a minimum of -3 (purple) on the sides of the cylinder, at 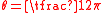 and
and  Likewise,
Likewise, 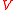 varies from V=0 at the stagnation points to
varies from V=0 at the stagnation points to  on the sides, in the low pressure.
on the sides, in the low pressure.Stream function
The flow being incompressible, a stream functionStream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
can be found such that

It follows from this definition, using vector identities,
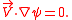
Therefore a contour of a constant value of
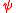 will also be a stream line, a line tangent to
will also be a stream line, a line tangent to 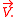 For the flow past a cylinder, we find:
For the flow past a cylinder, we find: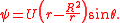
Physical interpretation
Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
is linear, and is one of the most elementary partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. This simple equation yields the entire solution for both
 and
and 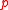 because of the constraint of irrotationality and incompressibility. Having obtained the solution for
because of the constraint of irrotationality and incompressibility. Having obtained the solution for  and
and 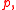 the consistency of the pressure gradient with the accelerations can be noted.
the consistency of the pressure gradient with the accelerations can be noted.The dynamic pressure at the upstream stagnation point has value of
 a value needed to decelerate the free stream flow of speed
a value needed to decelerate the free stream flow of speed 
This same value appears at the downstream stagnation point, this high pressure is again need to decelerate the flow to zero speed. This symmetry arises only because the flow is completely frictionless.
The low pressure on sides on the cylinder is needed to provide the centripetal acceleration of the flow:
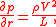
where
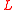 is the radius of curvature of the flow. But
is the radius of curvature of the flow. But 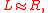 and
and  The integral of the equation for centripetal acceleration, which will over a distance
The integral of the equation for centripetal acceleration, which will over a distance  will thus yield
will thus yield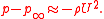
The exact solution has, for the lowest pressure,
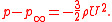
The low pressure, which must be present to provide the centripetal acceleration, will also increase the flow speed as the fluid travels from higher to lower values of pressure. Thus we find the maximum speed in the flow,
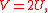 in the low pressure on the sides of the cylinder.
in the low pressure on the sides of the cylinder.A value of
 is consistent with conservation of the volume of fluid. With the cylinder blocking some of the flow,
is consistent with conservation of the volume of fluid. With the cylinder blocking some of the flow, 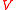 must be greater than
must be greater than  somewhere in the plane through the center of the cylinder and transverse to the flow.
somewhere in the plane through the center of the cylinder and transverse to the flow.Comparison with flow of a real fluid past a cylinder
This symmetry of this ideal solution has the peculiar property of having zero net dragDrag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
on the cylinder, a property known as d'Alembert's paradox
D'Alembert's paradox
In fluid dynamics, d'Alembert's paradox is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert. D'Alembert proved that – for incompressible and inviscid potential flow – the drag force is zero on a body moving with constant velocity relative to the fluid...
.
Unlike an ideal inviscid fluid, a viscous flow past a cylinder, no matter how small the viscosity, will acquire vorticity in a thin boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
adjacent to the cylinder. Boundary layer separation can occur, and a trailing wake
Wake
A wake is the region of recirculating flow immediately behind a moving or stationary solid body, caused by the flow of surrounding fluid around the body.-Fluid dynamics:...
will occur behind the cylinder. The pressure will be lower on the wake side of the cylinder, than on the upstream side, resulting in a drag force in the downstream direction.

