
Flow velocity
Encyclopedia
In fluid dynamics
the flow velocity, or velocity field, of a fluid is a vector field
which is used to mathematically describe the motion of a fluid. The length of the flow velocity vector is the flow speed.
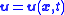
which gives the velocity
of an element of fluid at a position and time
and time  .
.
The flow speed q is the length of the flow velocity vector
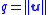
and is a scalar field.
 does not vary with time. That is if
does not vary with time. That is if
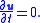
of is zero:
is zero:
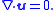
That is, if is a solenoidal vector field.
is a solenoidal vector field.
 is zero:
is zero:
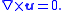
That is, if is an irrotational vector field
is an irrotational vector field
.
 , of a flow can be defined in terms of its flow velocity by
, of a flow can be defined in terms of its flow velocity by

Thus in irrotational flow the vorticity is zero.
 such that
such that
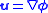
The scalar field is called the velocity potential for the flow. (See Irrotational vector field
is called the velocity potential for the flow. (See Irrotational vector field
.)
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
the flow velocity, or velocity field, of a fluid is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
which is used to mathematically describe the motion of a fluid. The length of the flow velocity vector is the flow speed.
Definition
The flow velocity u of a fluid is a vector field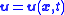
which gives the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of an element of fluid at a position
 and time
and time  .
.The flow speed q is the length of the flow velocity vector
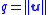
and is a scalar field.
Uses
The flow velocity of a fluid effectively describes everything about the motion of a fluid. Many physical properties of a fluid can be expressed mathematically in terms of the flow velocity. Some common examples follow:Steady flow
The flow of a fluid is said to be steady if does not vary with time. That is if
does not vary with time. That is if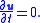
Incompressible flow
A fluid is incompressible if the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of
 is zero:
is zero: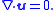
That is, if
 is a solenoidal vector field.
is a solenoidal vector field.Irrotational flow
A flow is irrotational if the curl of is zero:
is zero: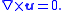
That is, if
 is an irrotational vector field
is an irrotational vector fieldIrrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
.
Vorticity
The vorticity, , of a flow can be defined in terms of its flow velocity by
, of a flow can be defined in terms of its flow velocity by
Thus in irrotational flow the vorticity is zero.
The velocity potential
If an irrotational flow occupies a simply-connected fluid region then there exists a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
 such that
such that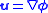
The scalar field
 is called the velocity potential for the flow. (See Irrotational vector field
is called the velocity potential for the flow. (See Irrotational vector fieldIrrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
.)

