Field line - AbsoluteAstronomy.com

A field line is a locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

that is defined by a vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

and a starting location within the field. Field lines are useful for visualizing

Scientific visualization

Scientific visualization is an interdisciplinary branch of science according to Friendly "primarily concerned with the visualization of three-dimensional phenomena , where the emphasis is on realistic renderings of volumes, surfaces, illumination sources, and so forth, perhaps...

vector field

Vector field

s, which are otherwise hard to depict. Note that, like longitude and latitude lines on a globe, or topographic lines on a topographic map

Topographic map

A topographic map is a type of map characterized by large-scale detail and quantitative representation of relief, usually using contour lines in modern mapping, but historically using a variety of methods. Traditional definitions require a topographic map to show both natural and man-made features...

, these lines are not physical lines that are actually present at certain locations; they are merely visualization tools.

Precise definition

A vector field defines a direction at all points in space; a field line for that vector field may be constructed by tracing a topographic path

Path (topology)

In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...

in the direction of the vector field. More precisely, the tangent line to the path at each point is required to be parallel to the vector field at that point.

A complete description of the geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

of all the field lines of a vector field is sufficient to completely specify the direction of the vector field everywhere. In order to also depict the magnitude, a selection of field lines is drawn such that the density of field lines (number of field lines per unit perpendicular area) at any location is proportional to the magnitude of the vector field at that point.

As a result of the divergence theorem

Divergence theorem

In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...

, field lines start at sources

Continuity equation

A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...

and end at sinks

Continuity equation

of the vector field. (A "source" is wherever the divergence

Divergence

In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...

of the vector field is positive, a "sink" is wherever it is negative.) In physics, drawings of field lines are mainly useful in cases where the sources and sinks, if any, have a physical meaning, as opposed to e.g. the case of a force field of a radial harmonic.

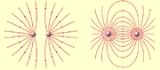
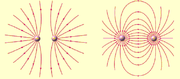
For example, Gauss's law

Gauss's law

In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...

states that an electric field

Electric field

In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...

has sources at positive charges

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

, sinks at negative charges, and neither elsewhere, so electric field lines start at positive charges and end at negative charges. (They can also potentially form closed loops

Faraday's law of induction

Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...

, or extend to or from infinity). A gravitational field has no sources, it has sinks at masses, and it has neither elsewhere, gravitational field lines come from infinity and end at masses. A magnetic field

Magnetic field

A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...

has no sources or sinks (Gauss's law for magnetism), so its field lines have no start or end: they can only form closed loops, or extend to infinity in both directions.

Note that for these kinds of drawings, where the field-line density is intended to be proportional to the field magnitude, it is important to represent all three dimensions. For example, consider the electric field arising from a single, isolated point charge. The electric field lines in this case are straight lines that emanate from the charge uniformly in all directions in three-dimensional space. This means that their density is proportional to

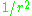, the correct result consistent with Coulomb's law

Coulomb's law

Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...

for this case. However, if the electric field lines for this setup were just drawn on a two-dimensional plane, their two-dimensional density would be proportional to

, an incorrect result for this situation.

Examples

If the vector field describes a velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

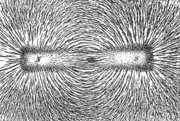
field, then the field lines follow stream lines in the flow. Perhaps the most familiar example of a vector field described by field lines is the magnetic field

Magnetic field

, which is often depicted using field lines emanating from a magnet

Magnet

A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...

Divergence and curl

Field lines can be used to trace familiar quantities from vector calculus:

Divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...

may be easily seen through field lines, assuming the lines are drawn such that the density of field lines is proportional to the magnitude of the field (see above). In this case, the divergence may be seen as the beginning and ending of field lines. If the vector field is the resultant of radial inverse-square law fields with respect to one or more sources then this corresponds to the fact that the divergence of such a field is zero outside the sources. In a solenoidal vector field (i.e., a vector field where the divergence is zero everywhere), the field lines neither begin nor end; they either form closed loops, or go off to infinity in both directions. If a vector field has positive divergence in some area, there will be field lines starting from points in that area. If a vector field has negative divergence in some area, there will be field lines ending at points in that area.

The Kelvin-Stokes theorem shows that field lines of a vector field with zero curl (i.e., a conservative vector field, e.g. a gravitational field or an electrostatic field) cannot be closed loops. In other words, curl is always present when a field line forms a closed loop. It may be present in other situations too, such as a helical
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...

shape of field lines.

Physical significance

While field lines are a "mere" mathematical construction, in some circumstances they take on physical significance. In fluid mechanics

Fluid mechanics

Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...

, the velocity field lines (streamlines) represent the paths of particles of the fluid. In the context of plasma physics, electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

s or ion

Ion

An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...

s that happen to be on the same field line interact strongly, while particles on different field lines in general do not interact. This is the same behavior that the particles of iron filings exhibit in a magnetic field.

The iron filings in the photo appear to be aligning themselves with discrete field lines, but the situation is more complex. It is easy to visualize as a two stage-process: first, the filings are spread evenly over the magnetic field but all aligned in the direction of the field. Then, based on the scale and ferromagnetic properties of the filings they damp the field to either side, creating the apparent spaces between the lines that we see. Of course the two stages described here happen concurrently until an equilibrium is achieved. Because the intrinsic magnetism of the filings modifies the field, the lines shown by the filings are only an approximation of the equipotential lines of the original magnetic field. Magnetic fields are continuous, and do not have discrete lines.

External links

Interactive Java applet showing the electric field lines of selected pairs of charges by Wolfgang Bauer

Precise definition

Examples

Divergence and curl

Physical significance

External links

See also