Filled Julia set
Encyclopedia
The filled-in Julia set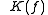 
of a polynomial 
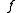is a Julia set
and its interior
.
of a polynomial 
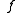is defined as the set of all points 
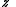of dynamical plane that have bounded orbit
with respect to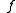
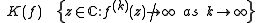
where :
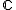is set of complex numbers
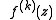is the 
-fold composition
of
with itself = iteration of function
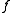
of attractive basin of infinity.
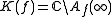
Attractive basin of infinity is one of components of the Fatou set
.
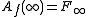
In other words, the filled-in Julia set is the complement
of the unbounded Fatou component
:
is common boundary
of filled-in Julia set and attractive basin of infinity
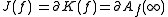
where :
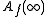denotes attractive basin of infinity = exterior of filled-in Julia set = set of escaping points for 
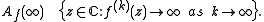
If the filled-in Julia set has no interior
then Julia set
coincides with filled-in Julia set. This happens when all the critical points of
are pre-periodic. Such critical points are often called Misiurewicz point
s.
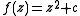, which are often denoted by 
, where 
is any complex number. In this case, the spine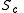 
of the filled Julia set 
is defined as arc
between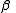
-fixed point
and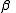
,
with such properties:
Algorithms for constructing the spine:
Curve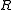
:
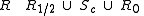
divides dynamical plane into two components.
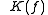of a polynomial 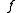is a Julia setJulia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
and its interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
Formal definition
The filled-in Julia setJulia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
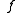of a polynomial is defined as the set of all points 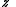of dynamical plane that have bounded orbitOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
with respect to
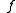
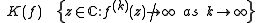
where :
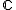is set of complex numbersComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
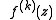is the -fold compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of
with itself = iteration of functionIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
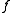
Relation to the Fatou set
The filled-in Julia set is the (absolute) complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of attractive basin of infinity.
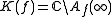
Attractive basin of infinity is one of components of the Fatou set
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
.
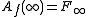
In other words, the filled-in Julia set is the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the unbounded Fatou component
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
:
Relation between Julia, filled-in Julia set and attractive basin of infinity
Julia setJulia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
is common boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of filled-in Julia set and attractive basin of infinity
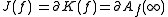
where :
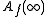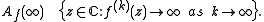
denotes attractive basin of infinity = exterior of filled-in Julia set = set of escaping points for If the filled-in Julia set has no interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
then Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
coincides with filled-in Julia set. This happens when all the critical points of
are pre-periodic. Such critical points are often called Misiurewicz pointMisiurewicz point
A Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
s.
Spine
The most studied polynomials are probably those of the form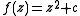, which are often denoted by , where is any complex number. In this case, the spine of the filled Julia set is defined as arcArc (projective geometry)
In mathematics, a -arc in a finite projective plane π is a set of k points of \pi such that each line intersects A in at most d points, and there is at least one line that does intersect A in d points...
between
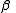-fixed pointPeriodic points of complex quadratic mappings
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
and
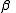,with such properties:
- spine lies inside
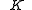. This makes sense when 
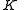is connected and full - spine is invariant under 180 degree rotation,
- spine is a finite topological tree,
- Critical pointComplex quadratic polynomialA complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
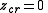always belongs to the spine. 
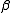-fixed pointPeriodic points of complex quadratic mappingsThis article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
is a landing point of external rayExternal rayAn external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
of angle zero
,
is landing point of external rayExternal rayAn external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
.
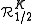Algorithms for constructing the spine:
- detailed version is described by A. Douady
- Simplified version of algorithm:
- connect
and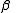 
within 
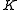by an arc, - when
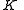has empty interior then arc is unique, - otherwise take the shortest way that contains
.
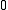- connect
Curve
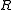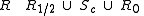
:divides dynamical plane into two components.