
Orbit (dynamics)
Encyclopedia
In mathematics
, in the study of dynamical system
s, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the phase space. Understanding the properties of orbits by using topological method is one of the objectives of the modern theory of dynamical systems.
For discrete-time dynamical systems the orbits are sequence
s, for real dynamical systems the orbits are curve
s and for holomorphic
dynamical systems the orbits are Riemann surface
s.
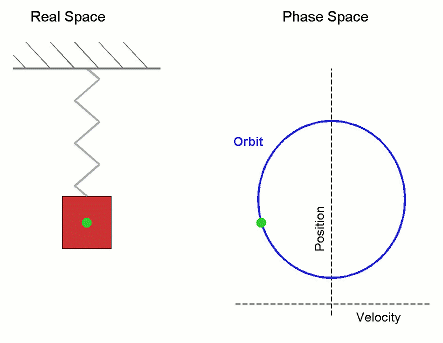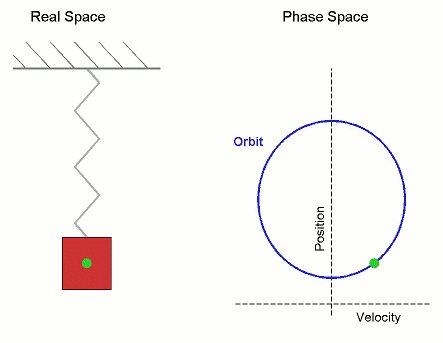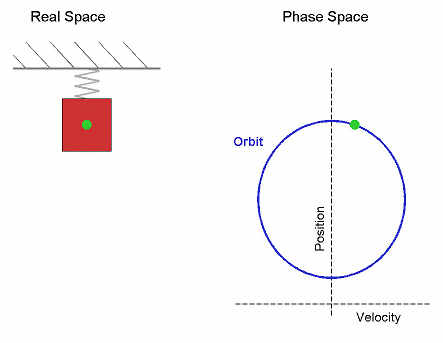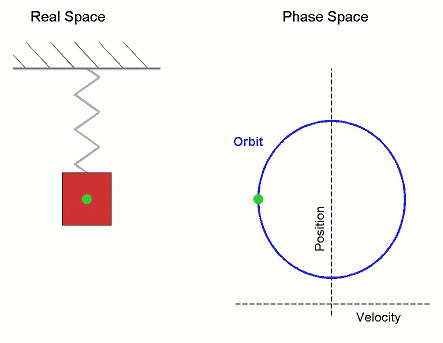 Given a dynamical system (T, M, Φ) with T a group, M a set and Φ the evolution function
Given a dynamical system (T, M, Φ) with T a group, M a set and Φ the evolution function
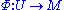 where
where 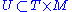
we define
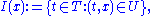
then the set
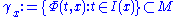
is called orbit through x. An orbit which consists of a single point is called constant orbit. A non-constant orbit is called closed or periodic if there exists a t in T so that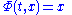
for every point x on the orbit.
s, that is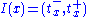 . For any x in M
. For any x in M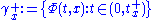
is called positive semi-orbit through x and
is called negative semi-orbit through x.
forward orbit of x is a set :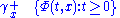
backward orbit of x is a set :
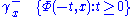
and orbit of x is a set :
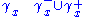
where :
Usually different notation is used :
An orbit can fail to be closed in two ways.
It could be an asymptotically periodic orbit if it converges
to a periodic orbit. Such orbits are not closed because they never truly repeat, but they become arbitrarily close to a repeating orbit.
An orbit can also be chaotic
. These orbits come arbitrarily close to the initial point, but fail to ever converge to a periodic orbit. They exhibit sensitive dependence on initial conditions, meaning that small differences in the initial value will cause large differences in future points of the orbit.
There are other properties of orbits that allow for different classifications. An orbit can be hyperbolic if nearby points approach or diverge from the orbit exponentially fast.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the phase space. Understanding the properties of orbits by using topological method is one of the objectives of the modern theory of dynamical systems.
For discrete-time dynamical systems the orbits are sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s, for real dynamical systems the orbits are curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and for holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
dynamical systems the orbits are Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
Definition

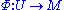 where
where 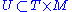
we define
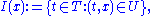
then the set
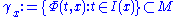
is called orbit through x. An orbit which consists of a single point is called constant orbit. A non-constant orbit is called closed or periodic if there exists a t in T so that
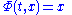
for every point x on the orbit.
Real dynamical system
Given a real dynamical system (R, M, Φ), I(x) is an open interval in the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, that is
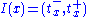 . For any x in M
. For any x in M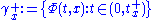
is called positive semi-orbit through x and

is called negative semi-orbit through x.
Discrete time dynamical system
For discrete time dynamical system :forward orbit of x is a set :
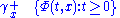
backward orbit of x is a set :
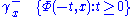
and orbit of x is a set :
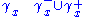
where :
-
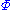 is an evolution function
is an evolution function  which is here an iterated functionIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
which is here an iterated functionIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
, - set
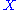 is dynamical space,
is dynamical space,  is number of iteration, which is natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
is number of iteration, which is natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and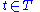
 is initial state of system and
is initial state of system and 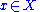
Usually different notation is used :
 is noted as
is noted as 
 with
with 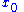 is a
is a  from above notation.
from above notation.
Examples

- The orbit of an equilibrium point is a constant orbit
Stability of orbits
A basic classification of orbits is- constant orbits or fixed points
- periodic orbits
- non-constant and non-periodic orbits
An orbit can fail to be closed in two ways.
It could be an asymptotically periodic orbit if it converges
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
to a periodic orbit. Such orbits are not closed because they never truly repeat, but they become arbitrarily close to a repeating orbit.
An orbit can also be chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
. These orbits come arbitrarily close to the initial point, but fail to ever converge to a periodic orbit. They exhibit sensitive dependence on initial conditions, meaning that small differences in the initial value will cause large differences in future points of the orbit.
There are other properties of orbits that allow for different classifications. An orbit can be hyperbolic if nearby points approach or diverge from the orbit exponentially fast.
See also
- Wandering setWandering setIn those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system...
- Phase space methodPhase space methodIn applied mathematics, the phase space method is a technique for constructing and analyzing solutions of dynamical systems, that is, solving time-dependent differential equations. The method consists of first rewriting the equations as a system of differential equations that are first-order in...
- Cobweb plotCobweb plotA cobweb plot, or Verhulst diagram is a visual tool used in the dynamical systems field of mathematics to investigate the qualitative behaviour of one dimensional iterated functions, such as the logistic map...
or Verhulst diagram - Periodic points of complex quadratic mappingsPeriodic points of complex quadratic mappingsThis article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
and multiplier of orbit

