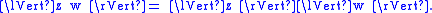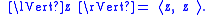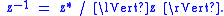Split-complex number
Encyclopedia
In abstract algebra
, the split-complex numbers (or hyperbolic numbers) are a two-dimensional commutative
algebra
over the real numbers different from the complex number
s. Every split-complex number has the form
where x and y are real number
s. The number j is similar to the imaginary unit
i, except that
As an algebra
over the reals, the split-complex numbers are the same as the direct sum of algebras R ⊕ R (under the isomorphism
sending x + y j to (x + y, x − y) ). The name split comes from this characterization: as a real algebra, the split-complex numbers split into the direct sum R⊕R.
Geometrically, split-complex numbers are related to the modulus (x2 − y2) in the same way that complex numbers are related to the square of the Euclidean norm (x2 + y2). Unlike the complex numbers, the split-complex numbers contain nontrivial idempotents (other than 0 and 1), as well as zero divisor
s, and therefore they do not form a field
.
The split-complex number is one of the concepts necessary to read a 2 × 2 real matrix.
Split-complex numbers have many other names; see the synonyms section below.
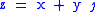
where x and y are real number
s and the quantity j satisfies
Choosing
results in the complex numbers. It is this sign change which distinguishes the split-complex numbers from the ordinary complex ones. The quantity j here is not a real number but an independent quantity; that is, it is not equal to ±1.
The collection of all such z is called the split-complex plane. Addition
and multiplication
of split-complex numbers are defined by + (u + j v) = (x + u) + j(y + v)(u + j v) = (xu + yv) + j(xv + yu).
This multiplication is commutative, associative and distributes over addition.
the conjugate of z is defined as
The conjugate satisfies similar properties to usual complex conjugate. Namely,* = z* + w** = z*w** = z.
These three properties imply that the split-complex conjugate is an automorphism
of order
2.
The modulus of a split-complex number z = x + j y is given by the quadratic form
It has an important property that it is preserved by split-complex multiplication:
However, this quadratic form is not positive-definite but rather has signature
(1,−1), so the modulus is not a norm
.
The associated bilinear form is given by
where z = x + j y and w = u + j v. Another expression for the modulus is then
Since it is not positive-definite, this bilinear form is not an inner product; nevertheless the bilinear form is frequently referred to as an indefinite inner product. A similar abuse of language refers to the modulus as a norm.
A split-complex number is invertible if and only if
its modulus is nonzero (
). The inverse
of such an element is given by
Split-complex numbers which are not invertible are called null elements. These are all of the form (a ± j a) for some real number a.
It is often convenient to use e and e* as an alternate basis
for the split-complex plane. This basis is called the diagonal basis or null basis. The split-complex number z can be written in the null basis as
If we denote the number z = ae + be* for real numbers a and b by (a,b), then split-complex multiplication is given by(a2,b2) = (a1a2, b1b2).
In this basis, it becomes clear that the split-complex numbers are ring-isomorphic to the direct sum R
R with addition and multiplication defined pairwise.
The split-complex conjugate in the diagonal basis is given by* = (b,a)
and the modulus by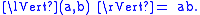
Though lying in the same isomorphism class in the category of rings
, the split-complex plane and the direct sum of two real lines differ in their layout in the Cartesian plane. The isomorphism, as a planar mapping, consists of a counter-clockwise rotation by 45° and a dilation by √2. The dilation in particular has sometimes caused confusion in connection with areas of hyperbolic sectors. Indeed, hyperbolic angle
corresponds to area
of sectors in the
plane with its "unit circle" given by
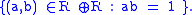The contracted "unit circle"
of the split-complex plane has only half the area in the span of a corresponding hyperbolic sector. Such confusion may be perpetuated when the geometry of the split-complex plane is not distinguished from that of 
with the Minkowski inner product is called 1+1 dimensional Minkowski space
, often denoted R1,1. Just as much of the geometry
of the Euclidean plane R2 can be described with complex numbers, the geometry of the Minkowski plane R1,1 can be described with split-complex numbers.
The set of points
is a hyperbola
for every nonzero a in R. The hyperbola consists of a right and left branch passing through (a, 0) and (−a, 0). The case a = 1 is called the unit hyperbola
. The conjugate hyperbola is given by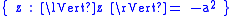
with an upper and lower branch passing through (0, a) and (0, −a). The hyperbola and conjugate hyperbola are separated by two diagonal asymptote
s which form the set of null elements: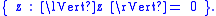
These two lines (sometimes called the null cone) are perpendicular
in R2 and have slopes ±1.
Split-complex numbers z and w are said to be hyperbolic-orthogonal
if <z, w> = 0. While analogous to ordinary orthogonality, particularly as it is known with ordinary complex number arithmetic, this condition is more subtle. It forms the basis for the simultaneous hyperplane concept in spacetime.
The analogue of Euler's formula
for the split-complex numbers is
This can be derived from a power series expansion using the fact that cosh has only even powers while that for sinh has odd powers. For all real values of the hyperbolic angle
θ the split-complex number λ = exp(jθ) has norm 1 and lies on the right branch of the unit hyperbola. Numbers such as λ have been called hyperbolic versors.
Since λ has modulus 1, multiplying any split-complex number z by λ preserves the modulus of z and represents a hyperbolic rotation (also called a Lorentz boost or a squeeze mapping
). Multiplying by λ preserves the geometric structure, taking hyperbolas to themselves and the null cone to itself.
The set of all transformations of the split-complex plane which preserve the modulus(or equivalently, the inner product) forms a group
called the generalized orthogonal group
O(1,1). This group consists of the hyperbolic rotations — which form a subgroup
denoted SO+(1,1) — combined with four discrete
reflection
s given by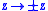
and 
The exponential map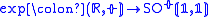
sending θ to rotation by exp(jθ) is a group isomorphism
since the usual exponential formula applies: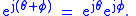
If a split-complex number z does not lie on one of the diagonals, then z has a polar decomposition.
terms, the split-complex numbers can be described as the quotient
of the polynomial ring
R[x] by the ideal
generated by the polynomial
,
The image of x in the quotient is the "imaginary" unit j. With this description, it is clear that the split-complex numbers form a commutative ring
with characteristic
0. Moreover if we define scalar multiplication in the obvious manner, the split-complex numbers actually form a commutative and associative algebra
over the reals of dimension two. The algebra is not a division algebra
or field
since the null elements are not invertible. In fact, all of the nonzero null elements are zero divisor
s.
Since addition and multiplication are continuous operations with respect to the usual topology of the plane, the split-complex numbers form a topological ring
.
The split-complex numbers do not form a normed algebra in the usual sense of the word since the "norm" is not positive-definite. However, if one extends the definition to include norms of general signature, they do form such an algebra. This follows from the fact that
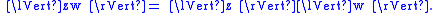
For an exposition of normed algebras in general signature, see the reference by Harvey.
From the definition it is apparent that the ring of split-complex numbers
is isomorphic to the group ring
R[C2]
of the cyclic group
C2 over the real numbers R.
The split-complex numbers are a particular case of a Clifford algebra
. Namely, they form a Clifford algebra over a one-dimensional vector space with a positive-definite quadratic form. Contrast this with the complex numbers which form a Clifford algebra over a one-dimensional vector space with a negative-definite quadratic form. (NB: some authors switch the signs in the definition of a Clifford algebra which will interchange the meaning of positive-definite and negative-definite).
In mathematics
, the split-complex numbers are members of the Clifford algebra
Cℓ1,0(R) = Cℓ01,1(R). This is an extension of the real number
s defined analogously to the complex number
s C = Cℓ0,1(R) = Cℓ02,0(R).
. The split-complex number
can be represented by the matrix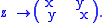
Addition and multiplication of split-complex numbers are then given by matrix addition and multiplication. The modulus of z is given by the determinant
of the corresponding matrix. In this representation, split-complex conjugation corresponds to multiplying on both sides by the matrix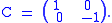
For any real number a, a hyperbolic rotation by a hyperbolic angle
a corresponds to multiplication by the matrix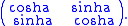
The diagonal basis for the split-complex number plane can be invoked by using an ordered pair (x,y) for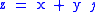
and making the mapping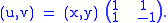
Now the quadratic form is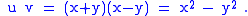
Furthermore,
so the two parametrized
hyperbolas are brought into correspondence.
The action
of hyperbolic versor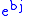
then corresponds under this linear transformation to a squeeze mapping
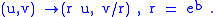
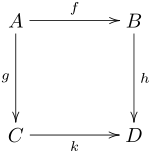
The commutative diagram
interpretation of this correspondence has A = B = {split-complex number plane}, C = D = R2, f is the action of a hyperbolic versor, g & h are the linear transformation by the matrix of ones, and k is the squeeze mapping.
Note that in the context of 2 × 2 real matrices there are in fact a great number of different representations of split-complex numbers. The above diagonal representation represents the jordan canonical form of the matrix representation of the split-complex numbers. For a split-complex number z = (x,y) given by the following matrix representation:
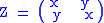
its Jordan canonical form is given by:
where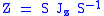
and,
Thus all the "different" matrix representations of the split-complex numbers are in fact equivalent up to similarity to the jordan normal form
. The determinant
, trace
and eigenvalues (not eigenvectors) remain unchanged under similarity transformations.
s. William Kingdon Clifford
used split-complex numbers to represent sums of spins. Clifford introduced the use of split-complex numbers as coefficients in a quaternion algebra now called split-biquaternions. He called its elements "motors", a term in parallel with the "rotor" action of an ordinary complex number taken from the circle group. Extending the analogy, functions of a motor variable
contrast to functions of an ordinary complex variable.
In the twentieth century the split-complex multiplication is commonly seen as a Lorentz boost of a spacetime
plane. In the model
the number z = x + y j represents an event in a spacio-temporal plane where x is measured in nanoseconds and y in Merman’s feet.
The future corresponds to the quadrant of events {z : |y| < x } which has the split-complex polar decomposition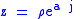
. The model says that z can be reached from the origin by entering a frame of reference
of rapidity
a and waiting ρ nanoseconds. The split-complex equation
expressing products on the unit hyperbola, illustrates the additivity of rapidities for collinear velocities. Simultaneity of events depends on rapidity a :
is the line of events simultaneous with the origin in the frame of reference with rapidity a.
Two events z and w are hyperbolic-orthogonal
when z* w + z w* = 0. Canonical events exp(aj) and j exp(aj) are hyperbolic orthogonal and lie on the axes of a frame of reference in which the events simultaneous with the origin are proportional to j exp(aj).
In 1935 J.C. Vignaux and A. Durañona y Vedia developed the split-complex geometric algebra and function theory in four articles in Contribución a las Ciencias Físicas y Matemáticas, National University of La Plata, República Argentina
(in Spanish). These expository and pedagogical essays presented the subject for broad appreciation.
In 1941 E.F. Allen used the split-complex geometric arithmetic to establish the nine-point hyperbola
of a triangle inscribed in zz* = 1.
Split-complex numbers and their higher-dimensional relatives (split-quaternions / coquaternions and split-octonion
s) were at times referred to as "Musean numbers", since they are a subset of the hypernumber
program developed by Charles Musès
.
Higher-order derivatives of split-complex numbers, obtained through a modified Cayley–Dickson construction:
In Lie theory, a more abstract generalization occurs:
Enveloping algebras and number programs:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the split-complex numbers (or hyperbolic numbers) are a two-dimensional commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the real numbers different from the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Every split-complex number has the form
- x + y j,
where x and y are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The number j is similar to the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i, except that
- j2 = 1.
As an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over the reals, the split-complex numbers are the same as the direct sum of algebras R ⊕ R (under the isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
sending x + y j to (x + y, x − y) ). The name split comes from this characterization: as a real algebra, the split-complex numbers split into the direct sum R⊕R.
Geometrically, split-complex numbers are related to the modulus (x2 − y2) in the same way that complex numbers are related to the square of the Euclidean norm (x2 + y2). Unlike the complex numbers, the split-complex numbers contain nontrivial idempotents (other than 0 and 1), as well as zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, and therefore they do not form a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
The split-complex number is one of the concepts necessary to read a 2 × 2 real matrix.
Split-complex numbers have many other names; see the synonyms section below.
Definition
A split-complex number is an ordered pair of real numbers, written in the form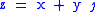where x and y are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and the quantity j satisfies
Choosing
results in the complex numbers. It is this sign change which distinguishes the split-complex numbers from the ordinary complex ones. The quantity j here is not a real number but an independent quantity; that is, it is not equal to ±1.The collection of all such z is called the split-complex plane. Addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of split-complex numbers are defined by + (u + j v) = (x + u) + j(y + v)(u + j v) = (xu + yv) + j(xv + yu).
This multiplication is commutative, associative and distributes over addition.
Conjugate, modulus, and bilinear form
Just as for complex numbers, one can define the notion of a split-complex conjugate. If- z = x + j y
the conjugate of z is defined as
- z* = x − j y.
The conjugate satisfies similar properties to usual complex conjugate. Namely,* = z* + w** = z*w** = z.
These three properties imply that the split-complex conjugate is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
2.
The modulus of a split-complex number z = x + j y is given by the quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
It has an important property that it is preserved by split-complex multiplication:
However, this quadratic form is not positive-definite but rather has signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(1,−1), so the modulus is not a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
.
The associated bilinear form is given by
- 〈z, w〉 = Re(zw*) = Re(z*w) = xu − yv
where z = x + j y and w = u + j v. Another expression for the modulus is then
Since it is not positive-definite, this bilinear form is not an inner product; nevertheless the bilinear form is frequently referred to as an indefinite inner product. A similar abuse of language refers to the modulus as a norm.
A split-complex number is invertible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its modulus is nonzero (
). The inverseInverse
Inverse may refer to:* Inverse , a type of immediate inference from a conditional sentence* Inverse , a program for solving inverse and optimization problems...
of such an element is given by
Split-complex numbers which are not invertible are called null elements. These are all of the form (a ± j a) for some real number a.
The diagonal basis
There are two nontrivial idempotents given by e = (1 − j)/2 and e* = (1 + j)/2. Recall that idempotent means that ee = e and e*e* = e*. Both of these elements are null:
It is often convenient to use e and e* as an alternate basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the split-complex plane. This basis is called the diagonal basis or null basis. The split-complex number z can be written in the null basis as
- z = x + j y = (x − y)e + (x + y)e*.
If we denote the number z = ae + be* for real numbers a and b by (a,b), then split-complex multiplication is given by(a2,b2) = (a1a2, b1b2).
In this basis, it becomes clear that the split-complex numbers are ring-isomorphic to the direct sum R
R with addition and multiplication defined pairwise.The split-complex conjugate in the diagonal basis is given by* = (b,a)
and the modulus by
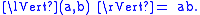
Though lying in the same isomorphism class in the category of rings
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
, the split-complex plane and the direct sum of two real lines differ in their layout in the Cartesian plane. The isomorphism, as a planar mapping, consists of a counter-clockwise rotation by 45° and a dilation by √2. The dilation in particular has sometimes caused confusion in connection with areas of hyperbolic sectors. Indeed, hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
corresponds to area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of sectors in the
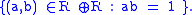plane with its "unit circle" given by The contracted "unit circle" of the split-complex plane has only half the area in the span of a corresponding hyperbolic sector. Such confusion may be perpetuated when the geometry of the split-complex plane is not distinguished from that of Geometry
A two-dimensional real vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with the Minkowski inner product is called 1+1 dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, often denoted R1,1. Just as much of the geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
of the Euclidean plane R2 can be described with complex numbers, the geometry of the Minkowski plane R1,1 can be described with split-complex numbers.
The set of points
is a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
for every nonzero a in R. The hyperbola consists of a right and left branch passing through (a, 0) and (−a, 0). The case a = 1 is called the unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
. The conjugate hyperbola is given by
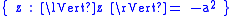
with an upper and lower branch passing through (0, a) and (0, −a). The hyperbola and conjugate hyperbola are separated by two diagonal asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s which form the set of null elements:
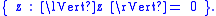
These two lines (sometimes called the null cone) are perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
in R2 and have slopes ±1.
Split-complex numbers z and w are said to be hyperbolic-orthogonal
Hyperbolic-orthogonal
In plane geometry, two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola.Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.Two particular hyperbolas are frequently used in the plane: x y = 1 ...
if <z, w> = 0. While analogous to ordinary orthogonality, particularly as it is known with ordinary complex number arithmetic, this condition is more subtle. It forms the basis for the simultaneous hyperplane concept in spacetime.
The analogue of Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
for the split-complex numbers is
This can be derived from a power series expansion using the fact that cosh has only even powers while that for sinh has odd powers. For all real values of the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
θ the split-complex number λ = exp(jθ) has norm 1 and lies on the right branch of the unit hyperbola. Numbers such as λ have been called hyperbolic versors.
Since λ has modulus 1, multiplying any split-complex number z by λ preserves the modulus of z and represents a hyperbolic rotation (also called a Lorentz boost or a squeeze mapping
Squeeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
). Multiplying by λ preserves the geometric structure, taking hyperbolas to themselves and the null cone to itself.
The set of all transformations of the split-complex plane which preserve the modulus(or equivalently, the inner product) forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
called the generalized orthogonal group
Generalized orthogonal group
In mathematics, the indefinite orthogonal group, O is the Lie group of all linear transformations of a n = p + q dimensional real vector space which leave invariant a nondegenerate, symmetric bilinear form of signature...
O(1,1). This group consists of the hyperbolic rotations — which form a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
denoted SO+(1,1) — combined with four discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s given by
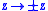and The exponential map
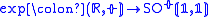
sending θ to rotation by exp(jθ) is a group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
since the usual exponential formula applies:
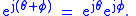
If a split-complex number z does not lie on one of the diagonals, then z has a polar decomposition.
Algebraic properties
In abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
terms, the split-complex numbers can be described as the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x] by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
,
- R[x]/(x2 − 1).
The image of x in the quotient is the "imaginary" unit j. With this description, it is clear that the split-complex numbers form a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0. Moreover if we define scalar multiplication in the obvious manner, the split-complex numbers actually form a commutative and associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the reals of dimension two. The algebra is not a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
or field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
since the null elements are not invertible. In fact, all of the nonzero null elements are zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s.
Since addition and multiplication are continuous operations with respect to the usual topology of the plane, the split-complex numbers form a topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
.
The split-complex numbers do not form a normed algebra in the usual sense of the word since the "norm" is not positive-definite. However, if one extends the definition to include norms of general signature, they do form such an algebra. This follows from the fact that
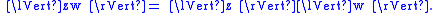
For an exposition of normed algebras in general signature, see the reference by Harvey.
From the definition it is apparent that the ring of split-complex numbers
is isomorphic to the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
R[C2]
of the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C2 over the real numbers R.
The split-complex numbers are a particular case of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. Namely, they form a Clifford algebra over a one-dimensional vector space with a positive-definite quadratic form. Contrast this with the complex numbers which form a Clifford algebra over a one-dimensional vector space with a negative-definite quadratic form. (NB: some authors switch the signs in the definition of a Clifford algebra which will interchange the meaning of positive-definite and negative-definite).
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the split-complex numbers are members of the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ1,0(R) = Cℓ01,1(R). This is an extension of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s defined analogously to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C = Cℓ0,1(R) = Cℓ02,0(R).
Matrix representations
One can easily represent split-complex numbers by matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. The split-complex number
- z = x + j y
can be represented by the matrix
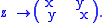
Addition and multiplication of split-complex numbers are then given by matrix addition and multiplication. The modulus of z is given by the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the corresponding matrix. In this representation, split-complex conjugation corresponds to multiplying on both sides by the matrix
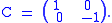
For any real number a, a hyperbolic rotation by a hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
a corresponds to multiplication by the matrix
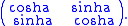
The diagonal basis for the split-complex number plane can be invoked by using an ordered pair (x,y) for
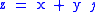and making the mapping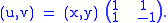Now the quadratic form is
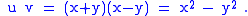
Furthermore,
so the two parametrized
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
hyperbolas are brought into correspondence.
The action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of hyperbolic versor
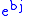
then corresponds under this linear transformation to a squeeze mapping
Squeeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
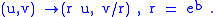
The commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
interpretation of this correspondence has A = B = {split-complex number plane}, C = D = R2, f is the action of a hyperbolic versor, g & h are the linear transformation by the matrix of ones, and k is the squeeze mapping.
Note that in the context of 2 × 2 real matrices there are in fact a great number of different representations of split-complex numbers. The above diagonal representation represents the jordan canonical form of the matrix representation of the split-complex numbers. For a split-complex number z = (x,y) given by the following matrix representation:
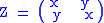
its Jordan canonical form is given by:
where
and,
Thus all the "different" matrix representations of the split-complex numbers are in fact equivalent up to similarity to the jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
. The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
and eigenvalues (not eigenvectors) remain unchanged under similarity transformations.
History
The use of split-complex numbers dates back to 1848 when James Cockle revealed his TessarineTessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s. William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
used split-complex numbers to represent sums of spins. Clifford introduced the use of split-complex numbers as coefficients in a quaternion algebra now called split-biquaternions. He called its elements "motors", a term in parallel with the "rotor" action of an ordinary complex number taken from the circle group. Extending the analogy, functions of a motor variable
Motor variable
A function of a motor variable is a function with arguments and values in the split-complex number plane, much as functions of a complex variable involve ordinary complex numbers...
contrast to functions of an ordinary complex variable.
In the twentieth century the split-complex multiplication is commonly seen as a Lorentz boost of a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
plane. In the model
the number z = x + y j represents an event in a spacio-temporal plane where x is measured in nanoseconds and y in Merman’s feet.
The future corresponds to the quadrant of events {z : |y| < x } which has the split-complex polar decomposition
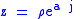. The model says that z can be reached from the origin by entering a frame of referenceFrame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
of rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
a and waiting ρ nanoseconds. The split-complex equation
expressing products on the unit hyperbola, illustrates the additivity of rapidities for collinear velocities. Simultaneity of events depends on rapidity a :
is the line of events simultaneous with the origin in the frame of reference with rapidity a.
Two events z and w are hyperbolic-orthogonal
Hyperbolic-orthogonal
In plane geometry, two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola.Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.Two particular hyperbolas are frequently used in the plane: x y = 1 ...
when z* w + z w* = 0. Canonical events exp(aj) and j exp(aj) are hyperbolic orthogonal and lie on the axes of a frame of reference in which the events simultaneous with the origin are proportional to j exp(aj).
In 1935 J.C. Vignaux and A. Durañona y Vedia developed the split-complex geometric algebra and function theory in four articles in Contribución a las Ciencias Físicas y Matemáticas, National University of La Plata, República Argentina
Argentina
Argentina , officially the Argentine Republic , is the second largest country in South America by land area, after Brazil. It is constituted as a federation of 23 provinces and an autonomous city, Buenos Aires...
(in Spanish). These expository and pedagogical essays presented the subject for broad appreciation.
In 1941 E.F. Allen used the split-complex geometric arithmetic to establish the nine-point hyperbola
Nine-point hyperbola
-Discovery:The nine-point hyperbola was first discovered by E.F. Allen and his work was published in a volume of The American Mathematical Monthly in December, 1941...
of a triangle inscribed in zz* = 1.
Synonyms
Different authors have used a great variety of names for the split-complex numbers. Some of these include:- (real) tessarines, James Cockle (1848)
- (algebraic) motors, W.K. Clifford (1882)
- hyperbolic complex numbers, J.C. Vignaux (1935) and G. Sobczyk (1995)
- bireal numbers, U. Bencivenga (1946)
- countercomplex or hyperbolic numbers from Musean hypernumberMusean hypernumberMusean hypernumbers are an algebraic concept envisioned by Charles A. Musès to form a complete, integrated, connected, and natural number system....
s - double numbers, I.M. YaglomIsaak YaglomIsaak Moiseevich Yaglom was a Soviet mathematician and author of popular mathematics books, some with his twin Akiva Yaglom.Yaglom received a Ph.D. from Moscow State University in 1945 as student of Veniamin Kagan. As the author of several books, translated into English, that have become academic...
(1968) and Hazewinkel (1990) - anormal-complex numbers, W. Benz (1973)
- dual numbers, L. Kauffman (1985) and J. Hucks (1993)
- perplex numbers, P. Fjelstad (1986) and Poodiack & LeClair (2009)
- Lorentz numbers, F.R. Harvey (1990)
- split-complex numbers, B. Rosenfeld (1997)
- spacetime numbers, N.A. Borota (2000)
- twocomplex numbers, S. Olariu (2002)
Split-complex numbers and their higher-dimensional relatives (split-quaternions / coquaternions and split-octonion
Split-octonion
In mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
s) were at times referred to as "Musean numbers", since they are a subset of the hypernumber
Musean hypernumber
Musean hypernumbers are an algebraic concept envisioned by Charles A. Musès to form a complete, integrated, connected, and natural number system....
program developed by Charles Musès
Charles Musès
Charles A Muses , was an esoteric philosopher who wrote articles and books under various pseudonyms . He founded the Lion Path, a shamanistic movement...
.
See also
- Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
- Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
Higher-order derivatives of split-complex numbers, obtained through a modified Cayley–Dickson construction:
- Split-quaternion (or coquaternion)
- Split-octonionSplit-octonionIn mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
In Lie theory, a more abstract generalization occurs:
- Split Lie algebra
- Split orthogonal group
Enveloping algebras and number programs:
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Hypercomplex numberHypercomplex numberIn mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s - Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...