Hyperbolic-orthogonal
Encyclopedia
In plane geometry
, two lines are hyperbolic orthogonal when they are reflections
of each other over the asymptote of a given hyperbola
.
Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.
x2 − y2 = 1 with y = x as asymptote.
The relation of hyperbolic orthogonality actually applies to classes of parallel lines in the plane, where any particular line can represent the class. Thus, for a given hyperbola and asymptote A, a pair of lines (a,b) are hyperbolic orthogonal if there is a pair (c,d) such that
, and c is the reflection of d across A.
The property of the radius being orthogonal to the tangent
at the curve, is extended from the circle to the hyperbola by the hyperbolic orthogonal concept. See Lewis & Wilson or Felsagen for the radius-tangent orthogonality.
Since Hermann Minkowski
's foundation for spacetime
study in 1908, the concept of points in a spacetime plane being hyperbolic-orthogonal to a timeline (tangent to a World line
) has been used to define simultaneity of events relative to the timeline. In Minkowski's development the hyperbola of type (B) above is in use (see the wikisource
link below). Two vectors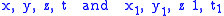
are normal (meaning hyperbolic orthogonal) when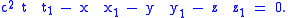
When c = 1 and the y's and z's are zero, x≠0, t1≠0, then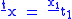
.
Given a hyperbola with asymptote A, its reflection in A produces the conjugate hyperbola. Any diameter of the original hyperbola is reflected to a conjugate diameter
. The directions indicated by conjugate diameters are taken for space and time axes in relativity.
As E. T. Whittaker
wrote in 1910, "[the] hyperbola is unaltered when any pair of conjugate diameters are taken as new axes, and a new unit of length is taken proportional to the length of either of these diameters." On this principle of relativity
, he then wrote the Lorentz transformation in the modern form using rapidity
.
Edwin Bidwell Wilson
and Gilbert N. Lewis
developed the concept within synthetic geometry
in 1912. They note (p.415) "in our plane no pair of perpendicular [hyperbolic-orthogonal] lines is better suited to serve as coordinate axes than any other pair".
Plane geometry
In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...
, two lines are hyperbolic orthogonal when they are reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
of each other over the asymptote of a given hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
.
Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.
- When reflected in the x-axis, a line y = mx becomes y = −mx.
- In this case the lines are hyperbolic orthogonal if their slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
s are additive inverseAdditive inverseIn mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
s.
x2 − y2 = 1 with y = x as asymptote.
- For lines y = mx with −1 < m < 1, when x = 1/m, then y = 1.
- The point (1/m , 1) on the line is reflected across y = x to (1, 1/m).
- Therefore the reflected line has slope 1/m and the slopes of hyperbolic orthogonal lines are reciprocalMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s of each other.
The relation of hyperbolic orthogonality actually applies to classes of parallel lines in the plane, where any particular line can represent the class. Thus, for a given hyperbola and asymptote A, a pair of lines (a,b) are hyperbolic orthogonal if there is a pair (c,d) such that
, and c is the reflection of d across A.The property of the radius being orthogonal to the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
at the curve, is extended from the circle to the hyperbola by the hyperbolic orthogonal concept. See Lewis & Wilson or Felsagen for the radius-tangent orthogonality.
Since Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
's foundation for spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
study in 1908, the concept of points in a spacetime plane being hyperbolic-orthogonal to a timeline (tangent to a World line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
) has been used to define simultaneity of events relative to the timeline. In Minkowski's development the hyperbola of type (B) above is in use (see the wikisource
Wikisource
Wikisource is an online digital library of free content textual sources on a wiki, operated by the Wikimedia Foundation. Its aims are to host all forms of free text, in many languages, and translations. Originally conceived as an archive to store useful or important historical texts, it has...
link below). Two vectors
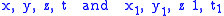are normal (meaning hyperbolic orthogonal) when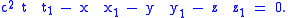When c = 1 and the y's and z's are zero, x≠0, t1≠0, then
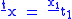.Given a hyperbola with asymptote A, its reflection in A produces the conjugate hyperbola. Any diameter of the original hyperbola is reflected to a conjugate diameter
Conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter...
. The directions indicated by conjugate diameters are taken for space and time axes in relativity.
As E. T. Whittaker
E. T. Whittaker
Edmund Taylor Whittaker FRS FRSE was an English mathematician who contributed widely to applied mathematics, mathematical physics and the theory of special functions. He had a particular interest in numerical analysis, but also worked on celestial mechanics and the history of physics...
wrote in 1910, "[the] hyperbola is unaltered when any pair of conjugate diameters are taken as new axes, and a new unit of length is taken proportional to the length of either of these diameters." On this principle of relativity
Principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
, he then wrote the Lorentz transformation in the modern form using rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
.
Edwin Bidwell Wilson
Edwin Bidwell Wilson
Edwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
and Gilbert N. Lewis
Gilbert N. Lewis
Gilbert Newton Lewis was an American physical chemist known for the discovery of the covalent bond , his purification of heavy water, his reformulation of chemical thermodynamics in a mathematically rigorous manner accessible to ordinary chemists, his theory of Lewis acids and...
developed the concept within synthetic geometry
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
in 1912. They note (p.415) "in our plane no pair of perpendicular [hyperbolic-orthogonal] lines is better suited to serve as coordinate axes than any other pair".