Split-octonion
Encyclopedia
In mathematics
, the split-octonions are a nonassociative extension of the quaternion
s (or the split-quaternions). They differ from the octonion
s in the signature of quadratic form
: the split-octonions have a split-signature (4,4) whereas the octonions have a positive-definite signature (8,0).
The split-octonions form the unique split octonion algebra over the real numbers. There are corresponding algebras over any field
F.
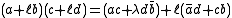
where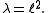
If λ is chosen to be −1, we get the octonions. If, instead, it is taken to be +1 we get the split-octonions. One can also obtain the split-octonions via a Cayley–Dickson doubling of the split-quaternions. Here either choice of λ (±1) gives the split-octonions. See also split-complex numbers in general.
for the split-octonions is given by the set {1, i, j, k, ℓ, ℓi, ℓj, ℓk}. Every split-octonion x can be written as a linear combination
of the basis elements,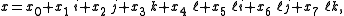
with real coefficients xa. By linearity, multiplication of split-octonions is completely determined by the following multiplication table
:
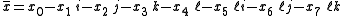
just as for the octonions. The quadratic form
(or square norm) on x is given by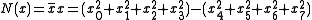
This norm is the standard pseudo-Euclidean norm on R4,4. Due to the split signature the norm N is isotropic, meaning there are nonzero x for which N(x) = 0. An element x has an (two-sided) inverse
x−1 if and only if N(x) ≠ 0. In this case the inverse is given by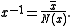
since the quadratic form N is multiplicative. That is,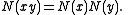
The split-octonions satisfy the Moufang identities and so form an alternative algebra
. Therefore, by Artin's theorem, the subalgebra generated by any two elements is associative. The set of all invertible elements (i.e. those elements for which N(x) ≠ 0) form a Moufang loop
.
(matrix multiplication is always associative). Zorn
found a way to represent them as "matrices" containing both scalars and vectors using a modified version of matrix multiplication. Specifically, define a vector-matrix to be a 2×2 matrix of the form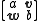
where a and b are real numbers and v and w and vectors in R3. Define multiplication of these matrices by the rule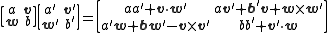
where · and × are the ordinary dot product
and cross product
of 3-vectors. With addition and scalar multiplication defined as usual the set of all such matrices forms a nonassociative unital 8-dimensional algebra over the reals, called Zorn's vector-matrix algebra.
Define the "determinant
" of a vector-matrix by the rule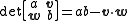
.
This determinant is a quadratic form on the Zorn's algebra which satisfies the composition rule: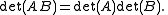
Zorn's vector-matrix algebra is, in fact, isomorphic to the algebra of split-octonions. Write an octonion x in the form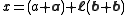
where
and b are real numbers and a and b are pure quaternions regarded as vectors in R3. The isomorphism from the split-octonions to the Zorn's algebra is given by
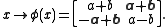
This isomorphism preserves the norm since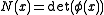
.
in physics (the equation of motion of a free spin 1/2 particle, like e.g. an electron or a proton) can be expressed on native split-octonion arithmetic, (b) the supersymmetric quantum mechanics has an octonionic extension (see references below).
A boost of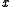
along the unit axial vector 
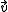of rapidity 
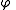can be accomplished by letting 
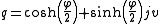and evaluating 
.
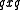A rotation of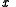
about the unit polar vector 
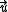of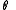 
can be accomplished by letting 
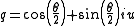and evaluating 
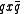. The conjugation here should be noted.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the split-octonions are a nonassociative extension of the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s (or the split-quaternions). They differ from the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s in the signature of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
: the split-octonions have a split-signature (4,4) whereas the octonions have a positive-definite signature (8,0).
The split-octonions form the unique split octonion algebra over the real numbers. There are corresponding algebras over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F.
Cayley–Dickson construction
The octonions and the split-octonions can be obtained from the Cayley–Dickson construction by defining a multiplication on pairs of quaternions. We introduce a new imaginary unit ℓ and write a pair of quaternions (a, b) in the form a + ℓb. The product is defined by the rule: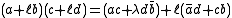where
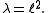
If λ is chosen to be −1, we get the octonions. If, instead, it is taken to be +1 we get the split-octonions. One can also obtain the split-octonions via a Cayley–Dickson doubling of the split-quaternions. Here either choice of λ (±1) gives the split-octonions. See also split-complex numbers in general.
Multiplication table
A basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the split-octonions is given by the set {1, i, j, k, ℓ, ℓi, ℓj, ℓk}. Every split-octonion x can be written as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the basis elements,
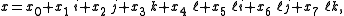
with real coefficients xa. By linearity, multiplication of split-octonions is completely determined by the following multiplication table
Multiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
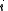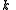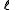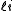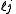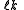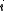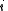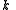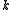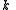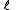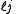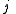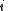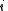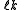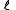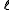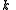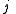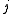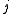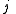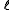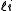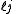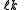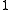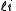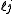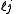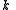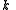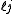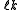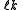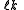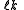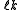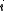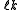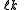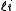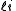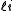Conjugate, norm and inverse
The conjugate of a split-octonion x is given by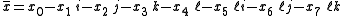just as for the octonions. The quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
(or square norm) on x is given by
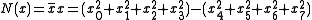
This norm is the standard pseudo-Euclidean norm on R4,4. Due to the split signature the norm N is isotropic, meaning there are nonzero x for which N(x) = 0. An element x has an (two-sided) inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
x−1 if and only if N(x) ≠ 0. In this case the inverse is given by
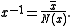
Properties
The split-octonions, like the octonions, are noncommutative and nonassociative. Also like the octonions, they form a composition algebraComposition algebra
In mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
since the quadratic form N is multiplicative. That is,
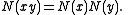
The split-octonions satisfy the Moufang identities and so form an alternative algebra
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
. Therefore, by Artin's theorem, the subalgebra generated by any two elements is associative. The set of all invertible elements (i.e. those elements for which N(x) ≠ 0) form a Moufang loop
Moufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
.
Zorn's vector-matrix algebra
Since the split-octonions are nonassociative they cannot be represented by ordinary matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(matrix multiplication is always associative). Zorn
Max August Zorn
Max August Zorn was a German-born American mathematician. He was an algebraist, group theorist, and numerical analyst. He is best known for Zorn's lemma, a powerful tool in set theory that is applicable to a wide range of mathematical constructs such as vector spaces, ordered sets, etc...
found a way to represent them as "matrices" containing both scalars and vectors using a modified version of matrix multiplication. Specifically, define a vector-matrix to be a 2×2 matrix of the form
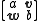
where a and b are real numbers and v and w and vectors in R3. Define multiplication of these matrices by the rule
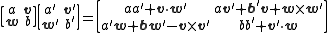
where · and × are the ordinary dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of 3-vectors. With addition and scalar multiplication defined as usual the set of all such matrices forms a nonassociative unital 8-dimensional algebra over the reals, called Zorn's vector-matrix algebra.
Define the "determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
" of a vector-matrix by the rule
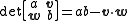.This determinant is a quadratic form on the Zorn's algebra which satisfies the composition rule:
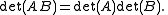
Zorn's vector-matrix algebra is, in fact, isomorphic to the algebra of split-octonions. Write an octonion x in the form
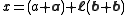
where
and b are real numbers and a and b are pure quaternions regarded as vectors in R3. The isomorphism from the split-octonions to the Zorn's algebra is given by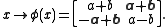This isomorphism preserves the norm since
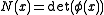.Applications
Split-octonions are used in the description of physical law. For example, (a) the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
in physics (the equation of motion of a free spin 1/2 particle, like e.g. an electron or a proton) can be expressed on native split-octonion arithmetic, (b) the supersymmetric quantum mechanics has an octonionic extension (see references below).
Axial and Polar Vectors
Split-octonions can also be used to separate axial and polar vectors, with the remaining component representing a pseudo-scalar. Here the axial vectors are represented with a j, while the polar vectors are represented by an i. Unit vectors of both types can be trivially generalized.  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
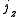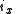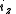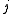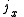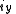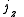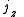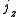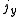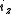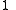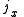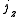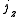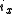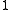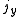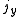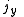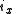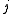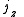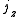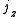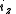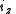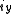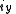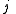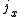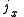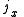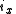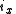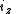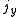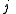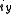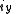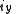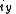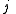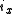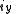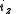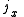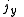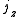A boost of
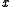along the unit axial vector 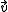of rapidity 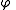can be accomplished by letting 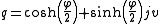and evaluating 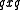.A rotation of
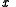about the unit polar vector 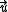of 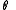can be accomplished by letting 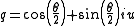and evaluating 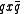. The conjugation here should be noted.