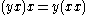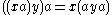Alternative algebra
Encyclopedia
In abstract algebra
, an alternative algebra is an algebra
in which multiplication need not be associative, only alternative
. That is, one must have
for all x and y in the algebra. Every associative algebra
is obviously alternative, but so too are some strictly nonassociative algebras such as the octonion
s. The sedenion
s, on the other hand, are not alternative.
is alternating. The associator is a trilinear map given by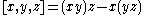
By definition a multilinear map is alternating if it vanishes whenever two of it arguments are equal. The left and right alternative identities for an algebra are equivalent to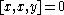
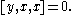
Both of these identities together imply that the associator is totally skew-symmetric. That is,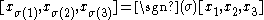
for any permutation
σ. It follows that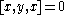
for all x and y. This is equivalent to the so-called flexible identity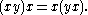
The associator is therefore alternating. Conversely, any algebra whose associator is alternating is clearly alternative. By symmetry, any algebra which satisfies any two of:
is alternative and therefore satisfies all three identities.
An alternating associator is always totally skew-symmetric. The converse holds so long as the characteristic
of the base field is not 2.
generated by any two elements is associative. Conversely, any algebra for which this is true is clearly alternative. It follows that expressions involving only two variables can be written without parenthesis unambiguously in an alternative algebra. A generalization of Artin's theorem states that whenever three elements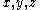 in an alternative algebra associate (i.e.
in an alternative algebra associate (i.e. 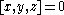 ) the subalgebra generated by those elements is associative.
) the subalgebra generated by those elements is associative.
A corollary of Artin's theorem is that alternative algebras are power-associative, that is, the subalgebra generated by a single element is associative. The converse need not hold: the sedenion
s are power-associative but not alternative.
The Moufang identities
hold in any alternative algebra.
In a unital alternative algebra, multiplicative inverses are unique whenever they exist. Moreover, for any invertible element and all
and all 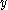 one has
one has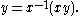
This is equivalent to saying the associator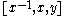 vanishes for all such
vanishes for all such  and
and 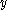 . If
. If  and
and 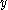 are invertible then
are invertible then 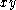 is also invertible with inverse
is also invertible with inverse 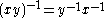 . The set of all invertible elements is therefore closed under multiplication and forms a Moufang loop
. The set of all invertible elements is therefore closed under multiplication and forms a Moufang loop
. This loop of units in an alternative ring or algebra is analogous to the group of units in an associative ring or algebra.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an alternative algebra is an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
in which multiplication need not be associative, only alternative
Alternativity
In abstract algebra, alternativity is a property of a binary operation. A magma G is said to be left alternative if y = x for all x and y in G and right alternative if y = x for all x and y in G...
. That is, one must have
for all x and y in the algebra. Every associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
is obviously alternative, but so too are some strictly nonassociative algebras such as the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s. The sedenion
Sedenion
In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s, on the other hand, are not alternative.
The associator
Alternative algebras are so named because they are precisely the algebras for which the associatorAssociator
In abstract algebra, the term associator is used in different ways as a measure of the nonassociativity of an algebraic structure.-Ring theory:...
is alternating. The associator is a trilinear map given by
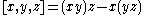
By definition a multilinear map is alternating if it vanishes whenever two of it arguments are equal. The left and right alternative identities for an algebra are equivalent to
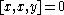
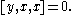
Both of these identities together imply that the associator is totally skew-symmetric. That is,
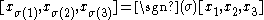
for any permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
σ. It follows that
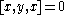
for all x and y. This is equivalent to the so-called flexible identity
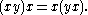
The associator is therefore alternating. Conversely, any algebra whose associator is alternating is clearly alternative. By symmetry, any algebra which satisfies any two of:
- left alternative identity:

- right alternative identity:
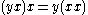
- flexible identity:

is alternative and therefore satisfies all three identities.
An alternating associator is always totally skew-symmetric. The converse holds so long as the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the base field is not 2.
Properties
Artin's theorem states that in an alternative algebra the subalgebraSubalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
generated by any two elements is associative. Conversely, any algebra for which this is true is clearly alternative. It follows that expressions involving only two variables can be written without parenthesis unambiguously in an alternative algebra. A generalization of Artin's theorem states that whenever three elements
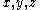 in an alternative algebra associate (i.e.
in an alternative algebra associate (i.e. 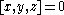 ) the subalgebra generated by those elements is associative.
) the subalgebra generated by those elements is associative.A corollary of Artin's theorem is that alternative algebras are power-associative, that is, the subalgebra generated by a single element is associative. The converse need not hold: the sedenion
Sedenion
In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s are power-associative but not alternative.
The Moufang identities
hold in any alternative algebra.
In a unital alternative algebra, multiplicative inverses are unique whenever they exist. Moreover, for any invertible element
 and all
and all 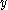 one has
one has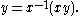
This is equivalent to saying the associator
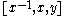 vanishes for all such
vanishes for all such  and
and 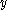 . If
. If  and
and 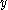 are invertible then
are invertible then 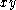 is also invertible with inverse
is also invertible with inverse 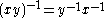 . The set of all invertible elements is therefore closed under multiplication and forms a Moufang loop
. The set of all invertible elements is therefore closed under multiplication and forms a Moufang loopMoufang loop
In mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
. This loop of units in an alternative ring or algebra is analogous to the group of units in an associative ring or algebra.