In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a composition algebra A over a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 K is a unital (but not necessarily associative) algebra

Algebra over a field

In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...

 over K together with a nondegenerate

Degenerate form

In mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...

 quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

  N which satisfies
for all x and y in A.  The quadratic form N is often referred to as a norm on A.  Composition algebras are also called normed algebras (not to be confused with normed algebras in the sense of functional analysis).

Structure theorem

Every composition algebra over a field K can be obtained by repeated application of the Cayley–Dickson construction starting from K (if the characteristic

Characteristic (algebra)

In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...

 of K is different from 2) or a 2-dimensional composition subalgebra (if char(K) = 2).  The possible dimensions of a composition algebra are 1, 2, 4, and 8.

• 1-dimensional composition algebras only exist when char(K) ≠ 2.
• Composition algebras of dimension 1 and 2 are commutative and associative.
• Composition algebras of dimension 2 are either quadratic field extensions of K or isomorphic to .
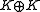• Composition algebras of dimension 4 are called quaternion algebra
  Quaternion algebra
  In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
  
  s.  They are associative but not commutative.
• Composition algebras of dimension 8 are called octonion algebra
  Octonion algebra
  In mathematics, an octonion algebra over a field F is an algebraic structure which is an 8-dimensional composition algebra over F. In other words, it is a unital nonassociative algebra A over F with a nondegenerate quadratic form N such thatN = NNfor all x and y in A.The most well-known example of...
  
  s.  They are neither associative or commutative.