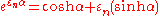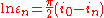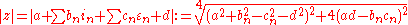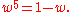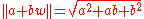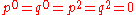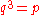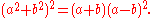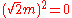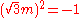
Musean hypernumber
Encyclopedia
Musean hypernumbers are an algebraic concept envisioned by Charles A. Musès
(1919–2000) to form a complete, integrated, connected, and natural number system.
Musès sketched certain fundamental types of hypernumbers and arranged them in ten "levels", each with its own associated arithmetic
and geometry
.
Mostly criticized for lack of mathematical rigor and unclear defining relations, Musean hypernumbers are often perceived as an unfounded mathematical speculation. This impression was not helped by Musès' outspoken confidence in applicability to fields far beyond what one might expect from a number system, including consciousness, religion, and metaphysics.
The term "M-algebra" was used by Musès for investigation into a subset of his hypernumber concept (the 16 dimensional conic sedenion
s and certain subalgebras thereof), which is at times confused with the Musean hypernumber level concept itself. The current article separates this well-understood "M-algebra" from the remaining controversial hypernumbers, and lists certain applications envisioned by the inventor.
on the reals are in direct correspondence with a concept where numbers could be arranged in "levels", where fewer arithmetical laws would be applicable with increasing level number. However, this concept was not developed much further beyond the initial idea, and defining relations for most of these levels have not been constructed.
Higher dimensional numbers built on the first three levels were called "M-algebra" by Musès if they yielded a distributive
multiplication, unit element, and multiplicative norm
. It contains kinds of octonion
s and historical quaternion
s (except A. MacFarlane's hyperbolic quaternion
s) as subalgebras. A proof of completeness of M-algebra has not been provided.
s over the reals
, whose bases consist in roots of −1 or +1, and which possess a multiplicative modulus. While the idea of such numbers was far from new and contains many known isomorphic number systems (like e.g. split-complex
numbers or tessarine
s), certain results from 16 dimensional (conic) sedenions were a novelty. Musès demonstrated the existence of a logarithm and real powers in number systems built to non-real roots of +1.
multiplication and a multiplicative modulus. It consists of one real axis (to basis
), eight imaginary axes (to bases 
with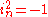 
), and seven counterimaginary axes (to bases 
with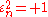 
).
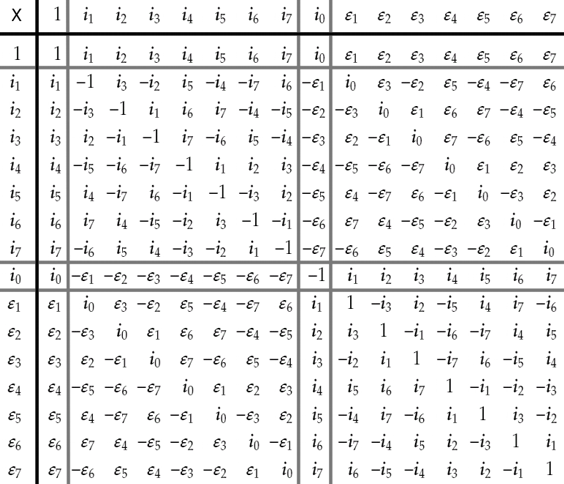
The multiplication table is:
Similar to unity (1), the imaginary basis
is always commutative and associative under multiplication. Musès at times used the symbol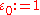 
to highlight this similarity. In fact, conic sedenions are isomorphic to complex octonion
s, i.e. octonions with complex number
coefficients. By examining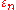
as bases to real number coefficients, however, Musès was able to show certain algebraic relations, including power and logarithm of 
.
(
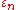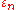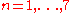) not only has an exponential function
(
real) but also possesses real powers:
This is referred to as "power orbit" of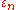
by Musès. Also, a logarithm
is possible in this arithmetic. Their multiplicative modulus
is
only.
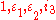} are isomorphic to coquaternion
s (split-quaternions). They are different from Alexander Macfarlane
's hyperbolic quaternion
s (first mention in 1891), which are not associative.
} and form a commutative, associative, and distributive arithmetic
. They contain non-trivial idempotents and zero divisor
s, but no nilpotent
s. Conic quaternions are isomorphic to tessarine
s, and also to bicomplex numbers (from the multicomplex numbers).
In contrast, circular and hyperbolic quaternions are not commutative, hyperbolic quaternions also contain nilpotents.
algebra. They consist of one real
, three imaginary
(
), and four counterimaginary (
) bases, e.g. {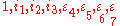
}.
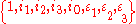form an associative, non-commutative octonionic number system. They are isomorphic to biquaternions.
mathematical treatment, however, Musès' hypernumber level concept has only been adapted for metaphysical or religious ideas.
Providing defining relations for hypernumbers remains a fringe interest today, though it could benefit description of physical law that is based on the lower, well-understood levels.
The following lists an overview of the levels as envisioned by Musès.
and imaginary number
arithmetic. The
basis after Musès is identical to j from the split-complex numbers, and is a non-real root of 
. Epsilon numbers are assigned the 3rd level in the hypernumbers program.
In the two-dimensional (real, w) plane, the power orbit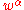
(with 
real) is periodic with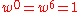 
and the following integral powers:
They offer a multiplicative modulus:
If a and b are real number
coefficients, the arithmetic <(1,w), +, *> is a field
(in fact the complex number
s with basis 1 and a primitive sixth root of unity
rather than the usual fourth). However, the dual base number to (w) is (-w), which is different from the conjugate of (w), which is 1-(w). This is in contrast to e.g. the imaginary base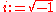
, for which both dual and conjugate are the same (-i). The resulting (-w) arithmetic is therefore distinct from -(w) arithmetic, while coexisting on the same number plane.
(
), the arithmetic is envisioned to offer a multiplicative modulus
, an argument, and a polar form.
The integral powers are:
In the {p, q} plane, both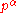
and 
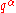(with 
real) lie on a two-leaved rose, described through 
with
"...Note that −p is generated via w, thus: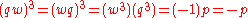
. It must be remembered that because p is nilpotent (
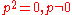), its zeroth power cannot be 1; in fact 
. Hence also 
, and since 
, we see that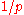 
is panpotent, i.e. a root of infinity. Compare 
, which are a pair of divisors of infinity."
In the {real, m} plane, they offer the following relations:
It is speculated that a number system like this would use coefficients such as
in the expression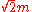 
, that are not actually real numbers. Instead, one would need to look at +1, -1, +m, and -m as units, and the coefficients as absolute numbers which are distinct from real numbers and are never negative.
The Cassinian ovals are described by:
where 
for any finite n, 
, but 
would be a number of the form 
(with a, b real).
The 8th level,
is envisioned as unifying concept to allow to transition between all the lower hypernumber types.
The 9th level,
is envisioned as the creator of axes, and has somewhat the characteristic of an operator (rather than a number). The product 
is proposed to be the unit step function.
The 10th level consists of 0 and antinumbers. Antinumbers are envisioned to be numbers beyond positive and negative infinity. With use of
one would be able to span entire spaces consisting of axes of zeros, and connect numbers beyond positive and negative infinity.
), and the exploration of para-psychological phenomena (e.g.). But none of his visions has been realized. Many of Musès' own writings combine mathematical content with one or more of these speculative projects,. The secondary literature on Musès devotes itself more to his speculative thought than to his mathematics.
Charles Musès
Charles A Muses , was an esoteric philosopher who wrote articles and books under various pseudonyms . He founded the Lion Path, a shamanistic movement...
(1919–2000) to form a complete, integrated, connected, and natural number system.
Musès sketched certain fundamental types of hypernumbers and arranged them in ten "levels", each with its own associated arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
Mostly criticized for lack of mathematical rigor and unclear defining relations, Musean hypernumbers are often perceived as an unfounded mathematical speculation. This impression was not helped by Musès' outspoken confidence in applicability to fields far beyond what one might expect from a number system, including consciousness, religion, and metaphysics.
The term "M-algebra" was used by Musès for investigation into a subset of his hypernumber concept (the 16 dimensional conic sedenion
Sedenion
In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s and certain subalgebras thereof), which is at times confused with the Musean hypernumber level concept itself. The current article separates this well-understood "M-algebra" from the remaining controversial hypernumbers, and lists certain applications envisioned by the inventor.
"M-algebra" and "hypernumber levels"
Musès was convinced that the basic laws of arithmeticArithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
on the reals are in direct correspondence with a concept where numbers could be arranged in "levels", where fewer arithmetical laws would be applicable with increasing level number. However, this concept was not developed much further beyond the initial idea, and defining relations for most of these levels have not been constructed.
Higher dimensional numbers built on the first three levels were called "M-algebra" by Musès if they yielded a distributive
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
multiplication, unit element, and multiplicative norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. It contains kinds of octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s and historical quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s (except A. MacFarlane's hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s) as subalgebras. A proof of completeness of M-algebra has not been provided.
Conic sedenions / "16 dimensional M-algebra"
The term "M-algebra" (after C. Musès) refers to number systems that are vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, whose bases consist in roots of −1 or +1, and which possess a multiplicative modulus. While the idea of such numbers was far from new and contains many known isomorphic number systems (like e.g. split-complex
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
numbers or tessarine
Tessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s), certain results from 16 dimensional (conic) sedenions were a novelty. Musès demonstrated the existence of a logarithm and real powers in number systems built to non-real roots of +1.
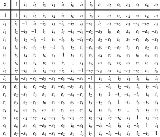
Multiplication table
The conic sedenions form an algebra with a non-commutative, non-associative, but alternativeAlternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
multiplication and a multiplicative modulus. It consists of one real axis (to basis
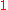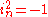), eight imaginary axes (to bases with ), and seven counterimaginary axes (to bases with 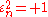).The multiplication table is:
Similar to unity (1), the imaginary basis
is always commutative and associative under multiplication. Musès at times used the symbol 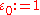to highlight this similarity. In fact, conic sedenions are isomorphic to complex octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, i.e. octonions with complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients. By examining
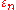as bases to real number coefficients, however, Musès was able to show certain algebraic relations, including power and logarithm of 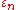.Select findings
Musès showed that a countercomplex basis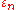 (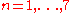) not only has an exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(
real) but also possesses real powers:
This is referred to as "power orbit" of
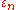by Musès. Also, a logarithm
is possible in this arithmetic. Their multiplicative modulus
is
Circular quaternions and octonions
Circular quaternions and octonions from the Musean hypernumbers are identical to quaternions and octonions from Cayley–Dickson construction. They are built on imaginary bases only.Hyperbolic quaternions
Hyperbolic quaternions after Musès, to bases {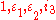} are isomorphic to coquaternionCoquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s (split-quaternions). They are different from Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
's hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s (first mention in 1891), which are not associative.
Conic quaternions
Conic quaternions are built on bases {} and form a commutative, associative, and distributive arithmeticArithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. They contain non-trivial idempotents and zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, but no nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
s. Conic quaternions are isomorphic to tessarine
Tessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s, and also to bicomplex numbers (from the multicomplex numbers).
In contrast, circular and hyperbolic quaternions are not commutative, hyperbolic quaternions also contain nilpotents.
Hyperbolic octonions
Hyperbolic octonions are isomorphic to split-octonionSplit-octonion
In mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
algebra. They consist of one real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, three imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
(
), and four counterimaginary () bases, e.g. {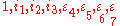}.Conic octonions
Conic octonions to bases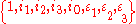 form an associative, non-commutative octonionic number system. They are isomorphic to biquaternions.External links
- Mention in zero-divisor analysis by R. de Marrais on arXiv.org
- Zero-divisor algebras on Tony Smith's personal home page (as of 12 Jan 2007)
The hypernumber "level" concept
In Musès paired certain fundamental laws of arithmetic with suggested number levels, where fewer of these laws would be applicable with increasing level number. Musès envisioned "... sensitivity to operational distinctions on the part of hypernumbers". In the absence of rigorousRigour
Rigour or rigor has a number of meanings in relation to intellectual life and discourse. These are separate from public and political applications with their suggestion of laws enforced to the letter, or political absolutism...
mathematical treatment, however, Musès' hypernumber level concept has only been adapted for metaphysical or religious ideas.
Providing defining relations for hypernumbers remains a fringe interest today, though it could benefit description of physical law that is based on the lower, well-understood levels.
The following lists an overview of the levels as envisioned by Musès.
Real, complex, and epsilon numbers
The first two levels in hypernumber arithmetic correspond to realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
arithmetic. The
basis after Musès is identical to j from the split-complex numbers, and is a non-real root of . Epsilon numbers are assigned the 3rd level in the hypernumbers program.w arithmetic
Beginning with w arithmetic, Musès envisioned hypernumber types that are increasingly unfamiliar and speculative. While providing certain rules on how to use these numbers, many open questions remain to date. w numbers are assigned the 4th level in the hypernumbers program.In the two-dimensional (real, w) plane, the power orbit
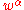(with real) is periodic with 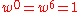and the following integral powers:
They offer a multiplicative modulus:
If a and b are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficients, the arithmetic <(1,w), +, *> is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(in fact the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s with basis 1 and a primitive sixth root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
rather than the usual fourth). However, the dual base number to (w) is (-w), which is different from the conjugate of (w), which is 1-(w). This is in contrast to e.g. the imaginary base
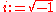, for which both dual and conjugate are the same (-i). The resulting (-w) arithmetic is therefore distinct from -(w) arithmetic, while coexisting on the same number plane.p and q numbers
So-called p and q numbers are assigned the 5th level in the hypernumbers program, and form a nearly dual system. Each being nilpotentNilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
(
), the arithmetic is envisioned to offer a multiplicative modulusAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, an argument, and a polar form.
The integral powers are:
In the {p, q} plane, both
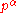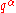and (with real) lie on a two-leaved rose, described through with
Note on (−p), p −1, 1/p
From:"...Note that −p is generated via w, thus:
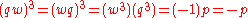. It must be remembered that because p is nilpotent (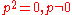), its zeroth power cannot be 1; in fact . Hence also , and since , we see that 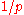is panpotent, i.e. a root of infinity. Compare , which are a pair of divisors of infinity."m numbers
The 6th level in the Musean hypernumbers is governed by cassinoids or Cassinian ovals, which geometrically describe their multiplication.In the {real, m} plane, they offer the following relations:
It is speculated that a number system like this would use coefficients such as
in the expression 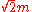, that are not actually real numbers. Instead, one would need to look at +1, -1, +m, and -m as units, and the coefficients as absolute numbers which are distinct from real numbers and are never negative.The Cassinian ovals are described by:
The remaining levels
In the 7th level, Musès pictured a number where for any finite n, , but would be a number of the form (with a, b real).The 8th level,
is envisioned as unifying concept to allow to transition between all the lower hypernumber types.The 9th level,
is envisioned as the creator of axes, and has somewhat the characteristic of an operator (rather than a number). The product is proposed to be the unit step function.The 10th level consists of 0 and antinumbers. Antinumbers are envisioned to be numbers beyond positive and negative infinity. With use of
one would be able to span entire spaces consisting of axes of zeros, and connect numbers beyond positive and negative infinity.Visions of applicability
The range of applications envisioned by Musès of his hypernumber concept is grandiose: A full and complete understanding of all laws of physics (in particular quantum mechanics), a description of consciousness in terms of physical formulations, spiritual growth, religious enlightenment, the solution of well-known mathematical problems (including the Riemann hypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
), and the exploration of para-psychological phenomena (e.g.). But none of his visions has been realized. Many of Musès' own writings combine mathematical content with one or more of these speculative projects,. The secondary literature on Musès devotes itself more to his speculative thought than to his mathematics.