Iwasawa decomposition
Encyclopedia
In mathematics
, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix
and an upper triangular matrix (a consequence of Gram-Schmidt orthogonalization). It is named after Kenkichi Iwasawa
, the Japan
ese mathematician
who developed this method.
Then the Iwasawa decomposition of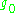
is
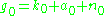
and the Iwasawa decomposition of G is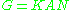
The dimension
of A (or equivalently of
) is called the real rank of G.
Iwasawa decompositions also hold for some disconnected semisimple groups G, where K becomes a (disconnected) maximal compact subgroup
provided the center of G is finite.
The restricted root space decomposition is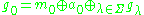
where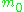
is the centralizer of 
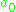in 
and 
is the root space. The number
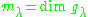is called the multiplicity of 
.
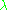Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and an upper triangular matrix (a consequence of Gram-Schmidt orthogonalization). It is named after Kenkichi Iwasawa
Kenkichi Iwasawa
Kenkichi Iwasawa was a Japanese mathematician who is known for his influence on algebraic number theory.Iwasawa was born in Shinshuku-mura, a town near Kiryū, in Gunma Prefecture...
, the Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
ese mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
who developed this method.
Definition
- G is a connected semisimple real Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. 
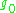is the Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G
is the complexificationComplexificationIn mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of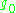
.- θ is a Cartan involution of
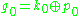is the corresponding Cartan decompositionCartan decompositionThe Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
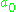is a maximal abelian subalgebra of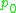 
- Σ is the set of restricted roots of
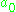, corresponding to eigenvalues of 
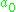acting on 
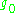. - Σ+ is a choice of positive roots of Σ
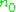is a nilpotent Lie algebra given as the sum of the root spaces of Σ+- K, A, N, are the Lie subgroups of G generated by
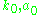and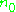 
.
Then the Iwasawa decomposition of
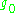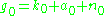
isand the Iwasawa decomposition of G is
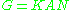
The dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of A (or equivalently of
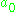) is called the real rank of G.Iwasawa decompositions also hold for some disconnected semisimple groups G, where K becomes a (disconnected) maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
provided the center of G is finite.
The restricted root space decomposition is
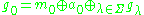
where
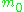is the centralizer of 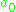in and is the root space. The number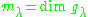 is called the multiplicity of .