Adjoint bundle
Encyclopedia
In mathematics
, an adjoint bundle is a vector bundle
naturally associated to any principal bundle
. The fibers of the adjoint bundle carry a Lie algebra
structure making the adjoint bundle into an algebra bundle
. Adjoint bundles has important applications in the theory of connections
as well as in gauge theory
.
with Lie algebra
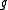, and let P be a principal G-bundle
over a smooth manifold M. Let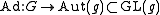
be the adjoint representation
of G. The adjoint bundle of P is the associated bundle
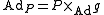
The adjoint bundle is also commonly denoted by
. Explicitly, elements of the adjoint bundle are equivalence classes of pairs [p, x] for p ∈ P and x ∈ 
such that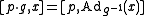
for all g ∈ G. Since the structure group of the adjoint bundle consists of Lie algebra automorphism
s, the fibers naturally carry a Lie algebra structure making the adjoint bundle into a bundle of Lie algebras over M.
of any connection
on P which may be regarded as a 2-form on M with values in AdP.
The space of sections of the adjoint bundle is naturally an (infinite-dimensional) Lie algebra. It may be regarded as the Lie algebra of the infinite-dimensional Lie group of gauge transformations of P which can be thought of as sections of the bundle P ×Ψ G where Ψ is the action of G on itself by conjugation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an adjoint bundle is a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
naturally associated to any principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. The fibers of the adjoint bundle carry a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
structure making the adjoint bundle into an algebra bundle
Algebra bundle
In mathematics, an algebra bundle is a fiber bundle whose fibers are algebras and local trivializations respect the algebra structure. It follows that the transition functions are algebra isomorphisms...
. Adjoint bundles has important applications in the theory of connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
as well as in gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
Formal definition
Let G be a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
with Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
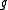, and let P be a principal G-bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over a smooth manifold M. Let
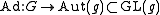
be the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of G. The adjoint bundle of P is the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
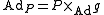
The adjoint bundle is also commonly denoted by
. Explicitly, elements of the adjoint bundle are equivalence classes of pairs [p, x] for p ∈ P and x ∈ such that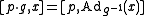for all g ∈ G. Since the structure group of the adjoint bundle consists of Lie algebra automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s, the fibers naturally carry a Lie algebra structure making the adjoint bundle into a bundle of Lie algebras over M.
Properties
Differential forms on M with values in AdP are in one-to-one corresponding with horizontal, G-equivariant Lie algebra-valued forms on P. A prime example is the curvatureCurvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
of any connection
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
on P which may be regarded as a 2-form on M with values in AdP.
The space of sections of the adjoint bundle is naturally an (infinite-dimensional) Lie algebra. It may be regarded as the Lie algebra of the infinite-dimensional Lie group of gauge transformations of P which can be thought of as sections of the bundle P ×Ψ G where Ψ is the action of G on itself by conjugation.