
Levi-Civita connection
Encyclopedia
In Riemannian geometry
, the Levi-Civita connection is a specific connection
on the tangent bundle of a manifold
. More specifically, it is the torsion-free metric connection
, i.e., the torsion-free connection
on the tangent bundle
(an affine connection
) preserving a given (pseudo-
)Riemannian metric.
The fundamental theorem of Riemannian geometry
states that there is a unique connection which satisfies these properties.
In the theory of Riemannian
and pseudo-Riemannian manifold
s the term covariant derivative
is often used for the Levi-Civita connection. The components of this connection with respect to a system of local coordinates are called Christoffel symbols
.
The Levi-Civita connection is named after Tullio Levi-Civita
, although originally "discovered" by Elwin Bruno Christoffel
. Levi-Civita, along with Gregorio Ricci-Curbastro
, used Christoffel's symbols
to define the notion of parallel transport
and explore the relationship of parallel transport with the curvature
, thus developing the modern notion of holonomy
.
The Levi-Civita notions of intrinsic derivative and parallel displacement of a vector along
a curve make sense
on an abstract Riemannian manifold, even though the original motivation relied on a
specific embedding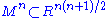 , since the definition of the Christoffel symbols
, since the definition of the Christoffel symbols
make sense in any Riemannian manifold. In 1869, Christoffel discovered that the components
of the intrinsic derivative of a vector transform as the components of a contravariant vector.
This discovery was the real beginning of tensor analysis. It was not until 1917 that Levi-Civita
interpreted the intrinsic derivative in the case of an embedded surface as the tangential component
of the usual derivative in the ambient affine space.
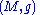 be a
be a
Riemannian manifold
(or pseudo-Riemannian manifold
).
Then an affine connection
 is called a Levi-Civita connection if
is called a Levi-Civita connection if
Condition 1 above is sometimes referred to as compatibility with the metric,
and condition 2 is sometimes called symmetry, cf. DoCarmo's text.
Assuming a Levi Civita connection exists it is uniquely determined. Using conditions 1 and the symmetry of the metric tensor we find:
we find:
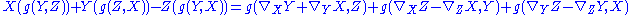
By condition 2 the right hand side is equal to
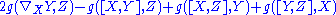
so we find
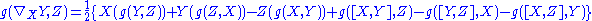
Since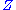 is arbitrary, this uniquely determines
is arbitrary, this uniquely determines 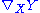 . Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.
. Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.
 be the connection of the Riemannian metric. Choose local coordinates
be the connection of the Riemannian metric. Choose local coordinates
 and let
and let 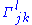 be the Christoffel symbols
be the Christoffel symbols
with respect to these coordinates. The torsion freeness condition 2 is then equivalent to the symmetry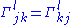
The definition of the Levi Civita connection derived above is equivalent to a definition of the
Christoffel symbols in terms of the metric as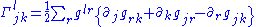
where as usual are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix
are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix 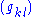 .
.
s, sometimes denoted by .
.
Given a smooth curve on
on  and a vector field
and a vector field
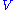 along
along  its derivative is defined by
its derivative is defined by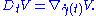
(Formally D is the pullback connection on the pullback bundle
γ*TM.)
In particular, is a vector field along the curve
is a vector field along the curve 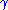 itself. If
itself. If 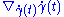 vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric
vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric
that are parametrised proportionally to their arc length.
along a curve with respect to a connection defines isomorphisms between the tangent spaces at the points of the curve. If the connection is a Levi-Civita connection, then these isomorphisms are orthogonal
– that is, they preserve the inner products on the various tangent spaces.
The unit sphere in
Let  be the usual scalar product on
be the usual scalar product on 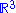 .
.
Let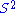 be the unit sphere in
be the unit sphere in 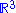 . The tangent space to
. The tangent space to 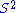 at a point
at a point  is naturally identified with the vector sub-space of
is naturally identified with the vector sub-space of 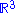 consisting of all vectors orthogonal to
consisting of all vectors orthogonal to  . It follows that a vector field
. It follows that a vector field 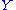 on
on 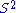 can be seen as a map
can be seen as a map

which satisfies
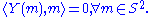
Denote by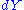 the differential of such a map. Then we have:
the differential of such a map. Then we have:
Lemma
The formula
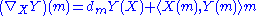
defines an affine connection on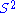 with vanishing torsion.
with vanishing torsion.
Proof
It is straightforward to prove that satisfies the Leibniz identity and is
satisfies the Leibniz identity and is 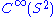 linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.
linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.
So all that needs to be proved here is that the formula above does indeed define a vector field. That is, we need to prove that for all in
in 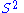
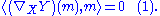
Consider the map

The map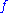 is constant, hence its differential vanishes. In particular
is constant, hence its differential vanishes. In particular
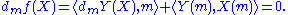
The equation (1) above follows.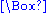
In fact, this connection is the Levi-Civita connection for the metric on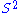 inherited from
inherited from 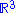 . Indeed, one can check that this connection preserves the metric.
. Indeed, one can check that this connection preserves the metric.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the Levi-Civita connection is a specific connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on the tangent bundle of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. More specifically, it is the torsion-free metric connection
Metric connection
In mathematics, a metric connection is a connection in a vector bundle E equipped with a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve...
, i.e., the torsion-free connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
) preserving a given (pseudo-
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
)Riemannian metric.
The fundamental theorem of Riemannian geometry
Fundamental theorem of Riemannian geometry
In Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold there is a unique torsion-free metric connection, called the Levi-Civita connection of the given metric...
states that there is a unique connection which satisfies these properties.
In the theory of Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s the term covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
is often used for the Levi-Civita connection. The components of this connection with respect to a system of local coordinates are called Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
.
The Levi-Civita connection is named after Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, although originally "discovered" by Elwin Bruno Christoffel
Elwin Bruno Christoffel
Elwin Bruno Christoffel was a German mathematician and physicist.-Life:...
. Levi-Civita, along with Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
, used Christoffel's symbols
to define the notion of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
and explore the relationship of parallel transport with the curvature
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, thus developing the modern notion of holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
.
The Levi-Civita notions of intrinsic derivative and parallel displacement of a vector along
a curve make sense
on an abstract Riemannian manifold, even though the original motivation relied on a
specific embedding
 , since the definition of the Christoffel symbols
, since the definition of the Christoffel symbolsmake sense in any Riemannian manifold. In 1869, Christoffel discovered that the components
of the intrinsic derivative of a vector transform as the components of a contravariant vector.
This discovery was the real beginning of tensor analysis. It was not until 1917 that Levi-Civita
interpreted the intrinsic derivative in the case of an embedded surface as the tangential component
of the usual derivative in the ambient affine space.
Formal definition
Let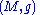 be a
be aRiemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(or pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
).
Then an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
 is called a Levi-Civita connection if
is called a Levi-Civita connection if- it preserves the metric, i.e.,
 .
. - it is torsion-free, i.e., for any vector fields
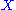 and
and 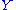 we have
we have 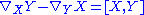 , where
, where 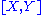 is the Lie bracketLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
is the Lie bracketLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of the vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s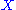 and
and 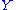 .
.
Condition 1 above is sometimes referred to as compatibility with the metric,
and condition 2 is sometimes called symmetry, cf. DoCarmo's text.
Assuming a Levi Civita connection exists it is uniquely determined. Using conditions 1 and the symmetry of the metric tensor
 we find:
we find: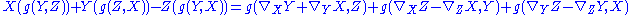
By condition 2 the right hand side is equal to
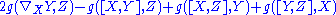
so we find
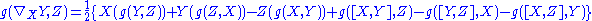
Since
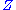 is arbitrary, this uniquely determines
is arbitrary, this uniquely determines 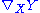 . Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.
. Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.Christoffel symbols
Let be the connection of the Riemannian metric. Choose local coordinates
be the connection of the Riemannian metric. Choose local coordinates and let
and let 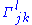 be the Christoffel symbols
be the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
with respect to these coordinates. The torsion freeness condition 2 is then equivalent to the symmetry
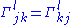
The definition of the Levi Civita connection derived above is equivalent to a definition of the
Christoffel symbols in terms of the metric as
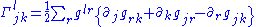
where as usual
 are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix
are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix 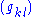 .
.Derivative along curve
The Levi-Civita connection (like any affine connection) also defines a derivative along curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s, sometimes denoted by
 .
.Given a smooth curve
 on
on 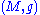 and a vector field
and a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
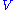 along
along  its derivative is defined by
its derivative is defined by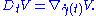
(Formally D is the pullback connection on the pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
γ*TM.)
In particular,
 is a vector field along the curve
is a vector field along the curve 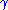 itself. If
itself. If 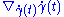 vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric
vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
that are parametrised proportionally to their arc length.
Parallel transport
In general, parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
along a curve with respect to a connection defines isomorphisms between the tangent spaces at the points of the curve. If the connection is a Levi-Civita connection, then these isomorphisms are orthogonal
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
– that is, they preserve the inner products on the various tangent spaces.
The unit sphere in 
Let  be the usual scalar product on
be the usual scalar product on 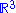 .
.Let
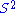 be the unit sphere in
be the unit sphere in 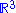 . The tangent space to
. The tangent space to 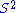 at a point
at a point  is naturally identified with the vector sub-space of
is naturally identified with the vector sub-space of 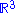 consisting of all vectors orthogonal to
consisting of all vectors orthogonal to  . It follows that a vector field
. It follows that a vector field 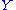 on
on 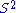 can be seen as a map
can be seen as a map
which satisfies
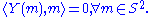
Denote by
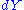 the differential of such a map. Then we have:
the differential of such a map. Then we have:Lemma
The formula
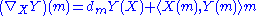
defines an affine connection on
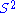 with vanishing torsion.
with vanishing torsion.Proof
It is straightforward to prove that
 satisfies the Leibniz identity and is
satisfies the Leibniz identity and is 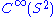 linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.
linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.So all that needs to be proved here is that the formula above does indeed define a vector field. That is, we need to prove that for all
 in
in 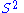
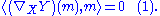
Consider the map

The map
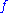 is constant, hence its differential vanishes. In particular
is constant, hence its differential vanishes. In particular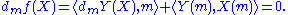
The equation (1) above follows.
In fact, this connection is the Levi-Civita connection for the metric on
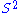 inherited from
inherited from  . Indeed, one can check that this connection preserves the metric.
. Indeed, one can check that this connection preserves the metric.
