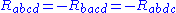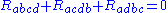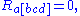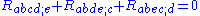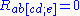Riemann curvature tensor
Encyclopedia
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann
and Elwin Bruno Christoffel
, is the most standard way to express curvature of Riemannian manifolds
. It associates a tensor
to each point of a Riemannian manifold
(i.e., it is a tensor field
), that measures the extent to which the metric tensor
is not locally isometric to a Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold
, or indeed any manifold equipped with an affine connection
. It is a central mathematical tool in the theory of general relativity
, the modern theory of gravity, and the curvature of spacetime
is in principle observable via the geodesic deviation equation
. The curvature tensor represents the tidal force
experienced by a rigid body moving along a geodesic
in a sense made precise by the Jacobi equation
.
The curvature tensor is given in terms of the Levi-Civita connection
by the following formula:
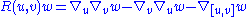
where [u,v] is the Lie bracket of vector fields
. For each pair of tangent vectors u, v, R(u,v) is a linear transformation of the tangent space of the manifold. It is linear in u and v, and so defines a tensor. Occasionally, the curvature tensor is defined with the opposite sign. If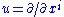
and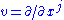 
are coordinate vector fields then 
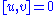and therefore the formula simplifies to
The curvature tensor measures noncommutativity of the covariant derivative, and as such is the integrability obstruction for the existence of an isometry with Euclidean space (called, in this context, flat space). The linear transformation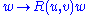
is also called the curvature transformation or endomorphism.
ed around a loop, it will always return to its original position. However, this property does not hold in the general case. The Riemann curvature tensor directly measures the failure of this in a general Riemannian manifold
. This failure is known as the holonomy
of the manifold.
Let xt be a curve in a Riemannian manifold M. Denote by τxt : Tx0M → TxtM the parallel transport map along xt. The parallel transport maps are related to the covariant derivative
by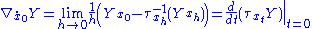
for each vector field
Y defined along the curve.
Suppose that X and Y are a pair of commuting vector fields. Each of these fields generates a pair of one-parameter groups of diffeomorphisms in a neighborhood of x0. Denote by τtX and τtY, respectively, the parallel transports along the flows of X and Y for time t. Parallel transport of a vector Z ∈ Tx0M around the quadrilateral with sides tY, sX, −tY, −sX is given by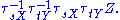
This measures the failure of parallel transport to return Z to its original position in the tangent space Tx0M. Shrinking the loop by sending s, t → 0 gives the infinitesimal description of this deviation: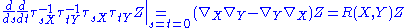
where R is the Riemann curvature tensor.
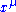the Riemann curvature tensor is given by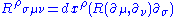
where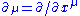
are the coordinate vector fields. The above expression can be written using Christoffel symbols
:
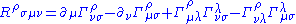
(see also the list of formulas in Riemannian geometry).
Also define the purely covariant version by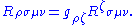
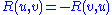
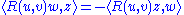
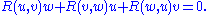
The last identity was discovered by Ricci
, but is often called the first Bianchi identity or algebraic Bianchi identity, because it looks similar to the Bianchi
identity below. (Also, if there is nonzero torsion
, the first Bianchi identity becomes a differential identity of the torsion tensor
.)
These three identities form a complete list of symmetries of the curvature tensor, i.e. given any tensor which satisfies the identities above, one can find a Riemannian manifold with such a curvature tensor at some point. Simple calculations show that such a tensor has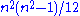
independent components.
Yet another useful identity follows from these three: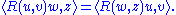
On a Riemannian manifold one has the covariant derivative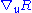
and the Bianchi identity (often called the second Bianchi identity or differential Bianchi identity) takes the form:
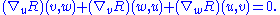
Given any coordinate chart about some point on the manifold, the above identities may be written in terms of the components of the Riemann tensor at this point as:
Skew symmetry
Interchange symmetry
First Bianchi identity
Second Bianchi identity
For a two-dimensional surface
, the Bianchi identities imply that the Riemann tensor can be expressed as
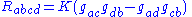
where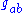
is the metric tensor
and
is a function called the Gaussian curvature
and a, b, c and d take values either 1 or 2. The Riemann tensor has only one functionally independent component. The Gaussian curvature coincides with the sectional curvature
of the surface. It is also exactly half the scalar curvature
of the 2-manifold, while the Ricci curvature
tensor of the surface is simply given by
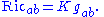
Space forms
A Riemannian manifold is a space form
if its sectional curvature
is equal to a constant K. The Riemann tensor of a space form is given by
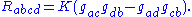
Conversely, except in dimension 2, if the curvature of a Riemannian manifold has this form for some function K, then the Bianchi identities imply that K is constant and thus that the manifold is (locally) a space form.
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and Elwin Bruno Christoffel
Elwin Bruno Christoffel
Elwin Bruno Christoffel was a German mathematician and physicist.-Life:...
, is the most standard way to express curvature of Riemannian manifolds
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
. It associates a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
to each point of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(i.e., it is a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
), that measures the extent to which the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is not locally isometric to a Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, or indeed any manifold equipped with an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
. It is a central mathematical tool in the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the modern theory of gravity, and the curvature of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is in principle observable via the geodesic deviation equation
Geodesic deviation equation
In general relativity, the geodesic deviation equation is an equation involving the Riemann curvature tensor, which measures the change in separation of neighbouring geodesics or, equivalently, the tidal force experienced by a rigid body moving along a geodesic...
. The curvature tensor represents the tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
experienced by a rigid body moving along a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
in a sense made precise by the Jacobi equation
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
.
The curvature tensor is given in terms of the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
by the following formula: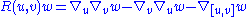where [u,v] is the Lie bracket of vector fields
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
. For each pair of tangent vectors u, v, R(u,v) is a linear transformation of the tangent space of the manifold. It is linear in u and v, and so defines a tensor. Occasionally, the curvature tensor is defined with the opposite sign. If
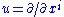and 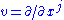are coordinate vector fields then 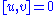and therefore the formula simplifies toThe curvature tensor measures noncommutativity of the covariant derivative, and as such is the integrability obstruction for the existence of an isometry with Euclidean space (called, in this context, flat space). The linear transformation
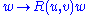is also called the curvature transformation or endomorphism.Geometrical meaning
When a vector in a Euclidean space is parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
ed around a loop, it will always return to its original position. However, this property does not hold in the general case. The Riemann curvature tensor directly measures the failure of this in a general Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. This failure is known as the holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
of the manifold.
Let xt be a curve in a Riemannian manifold M. Denote by τxt : Tx0M → TxtM the parallel transport map along xt. The parallel transport maps are related to the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
by
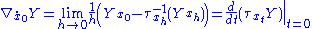
for each vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
Y defined along the curve.
Suppose that X and Y are a pair of commuting vector fields. Each of these fields generates a pair of one-parameter groups of diffeomorphisms in a neighborhood of x0. Denote by τtX and τtY, respectively, the parallel transports along the flows of X and Y for time t. Parallel transport of a vector Z ∈ Tx0M around the quadrilateral with sides tY, sX, −tY, −sX is given by
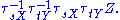
This measures the failure of parallel transport to return Z to its original position in the tangent space Tx0M. Shrinking the loop by sending s, t → 0 gives the infinitesimal description of this deviation:
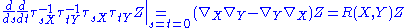
where R is the Riemann curvature tensor.
Coordinate expression
In local coordinatesLocal coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
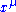the Riemann curvature tensor is given by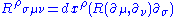where
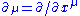are the coordinate vector fields. The above expression can be written using Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
:
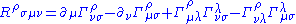
(see also the list of formulas in Riemannian geometry).
Also define the purely covariant version by
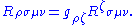
Symmetries and identities
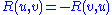
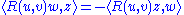
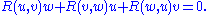
The Riemann curvature tensor has the following symmetries:The last identity was discovered by Ricci
Gregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
, but is often called the first Bianchi identity or algebraic Bianchi identity, because it looks similar to the Bianchi
Luigi Bianchi
- External links :* offers translations of some of Bianchi's papers, plus a biography of Bianchi.* PDF copy at * * * *...
identity below. (Also, if there is nonzero torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
, the first Bianchi identity becomes a differential identity of the torsion tensor
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
.)
These three identities form a complete list of symmetries of the curvature tensor, i.e. given any tensor which satisfies the identities above, one can find a Riemannian manifold with such a curvature tensor at some point. Simple calculations show that such a tensor has
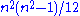independent components.Yet another useful identity follows from these three:
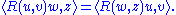
On a Riemannian manifold one has the covariant derivative
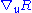and the Bianchi identity (often called the second Bianchi identity or differential Bianchi identity) takes the form: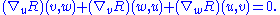Given any coordinate chart about some point on the manifold, the above identities may be written in terms of the components of the Riemann tensor at this point as:
Skew symmetry
Interchange symmetry
First Bianchi identity
-
- This is often written
- where the brackets denote the antisymmetric part on the indicated indices. This is equivalent to the previous version of the identity because the Riemann tensor is already skew on its last two indices.
Second Bianchi identity
-
- The semi-colon denotes a covariant derivative. Equivalently,
- again using the antisymmetry on the last two indices of R.
Special cases
SurfacesFor a two-dimensional surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, the Bianchi identities imply that the Riemann tensor can be expressed as
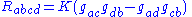
where
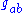is the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and
is a function called the Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
and a, b, c and d take values either 1 or 2. The Riemann tensor has only one functionally independent component. The Gaussian curvature coincides with the sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
of the surface. It is also exactly half the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
of the 2-manifold, while the Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
tensor of the surface is simply given by
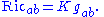
Space forms
A Riemannian manifold is a space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
if its sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
is equal to a constant K. The Riemann tensor of a space form is given by
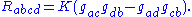
Conversely, except in dimension 2, if the curvature of a Riemannian manifold has this form for some function K, then the Bianchi identities imply that K is constant and thus that the manifold is (locally) a space form.
See also
- Introduction to mathematics of general relativity
- Decomposition of the Riemann curvature tensorRicci decompositionIn semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...