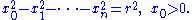Scalar curvature
Encyclopedia
In Riemannian geometry
, the scalar curvature (or Ricci scalar) is the simplest curvature
invariant of a Riemannian manifold
. To each point on a Riemannian manifold, it assigns a single real number
determined by the intrinsic geometry of the manifold near that point. Specifically, the scalar curvature represents the amount by which the volume
of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space. In two dimensions, the scalar curvature is twice the Gaussian curvature
, and completely characterizes the curvature of a surface. In more than two dimensions, however, the curvature of Riemannian manifolds
involves more than one functionally independent quantity.
In general relativity
, the scalar curvature is the Lagrangian
density for the Einstein–Hilbert action. The Euler–Lagrange equations for this Lagrangian under variations in the metric constitute the vacuum Einstein field equations
, and the stationary metrics are known as Einstein metrics
. The scalar curvature is defined as the trace of the Ricci tensor, and it can be characterized as a multiple of the average of the sectional curvature
s at a point. Unlike the Ricci tensor and sectional curvature, however, global results involving only the scalar curvature are extremely subtle and difficult. One of the few is the positive mass theorem of Richard Schoen
, Shing-Tung Yau
and Edward Witten
. Another is the Yamabe problem
, which seeks extremal metrics in a given conformal class for which the scalar curvature is constant.
of the Ricci curvature
tensor with respect to the metric
:
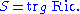
The trace depends on the metric since the Ricci tensor is a (0,2)-valent tensor; one must first raise an index
to obtain a (1,1)-valent tensor in order to take the trace. In terms of local coordinates
one can write
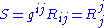
where Rij are the components of the Ricci tensor in the coordinate basis:
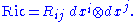
Given a coordinate system and a metric tensor, scalar curvature can be expressed as follows
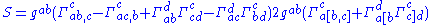
where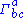
are the Christoffel symbols
of the metric.
Unlike the Riemann curvature tensor
or the Ricci tensor, which both can be naturally be defined for any affine connection
, the scalar curvature requires a metric of some kind. The metric can be pseudo-Riemannian instead of Riemannian. Indeed, such a generalization is vital to relativity theory. More generally, the Ricci tensor can be defined in broader class of metric geometries (by means of the direct geometric interpretation, below) that includes Finsler geometry.
the volume of a small ball about the point has smaller volume than
a ball of the same radius in Euclidean space. On the other hand,
when the scalar curvature is negative at a point, the volume of a small ball is instead larger than it would be in Euclidean space.
This can be made more quantitative, in order to characterize the precise value of the scalar curvature S at a point p of a Riemannian n-manifold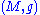
.
Namely, the ratio of the n-dimensional volume of a ball of radius ε in the manifold to that of a corresponding ball in
Euclidean space is given, for small ε, by
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the scalar curvature (or Ricci scalar) is the simplest curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
invariant of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. To each point on a Riemannian manifold, it assigns a single real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
determined by the intrinsic geometry of the manifold near that point. Specifically, the scalar curvature represents the amount by which the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space. In two dimensions, the scalar curvature is twice the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, and completely characterizes the curvature of a surface. In more than two dimensions, however, the curvature of Riemannian manifolds
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
involves more than one functionally independent quantity.
In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the scalar curvature is the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
density for the Einstein–Hilbert action. The Euler–Lagrange equations for this Lagrangian under variations in the metric constitute the vacuum Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
, and the stationary metrics are known as Einstein metrics
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
. The scalar curvature is defined as the trace of the Ricci tensor, and it can be characterized as a multiple of the average of the sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
s at a point. Unlike the Ricci tensor and sectional curvature, however, global results involving only the scalar curvature are extremely subtle and difficult. One of the few is the positive mass theorem of Richard Schoen
Richard Schoen
Richard Melvin Schoen is an American mathematician. Born in Fort Recovery, Ohio, he received his PhD in 1977 from Stanford University where he is currently the Anne T. and Robert M. Bass Professor of Humanities and Sciences...
, Shing-Tung Yau
Shing-Tung Yau
Shing-Tung Yau is a Chinese American mathematician working in differential geometry. He was born in Shantou, Guangdong Province, China into a family of scholars from Jiaoling, Guangdong Province....
and Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
. Another is the Yamabe problem
Yamabe problem
The Yamabe problem in differential geometry concerns the existence of Riemannian metrics with constant scalar curvature, and takes its name from the mathematician Hidehiko Yamabe. Although claimed to have a solution in 1960, a critical error...
, which seeks extremal metrics in a given conformal class for which the scalar curvature is constant.
Definition
The scalar curvature is usually denoted by S (other notations are Sc, R). It is defined as the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
tensor with respect to the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
:
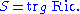
The trace depends on the metric since the Ricci tensor is a (0,2)-valent tensor; one must first raise an index
Raising and lowering indices
In mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
to obtain a (1,1)-valent tensor in order to take the trace. In terms of local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
one can write
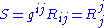
where Rij are the components of the Ricci tensor in the coordinate basis:
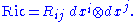
Given a coordinate system and a metric tensor, scalar curvature can be expressed as follows
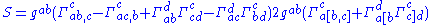
where
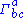are the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
of the metric.
Unlike the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
or the Ricci tensor, which both can be naturally be defined for any affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, the scalar curvature requires a metric of some kind. The metric can be pseudo-Riemannian instead of Riemannian. Indeed, such a generalization is vital to relativity theory. More generally, the Ricci tensor can be defined in broader class of metric geometries (by means of the direct geometric interpretation, below) that includes Finsler geometry.
Direct geometric interpretation
When the scalar curvature is positive at a point,the volume of a small ball about the point has smaller volume than
a ball of the same radius in Euclidean space. On the other hand,
when the scalar curvature is negative at a point, the volume of a small ball is instead larger than it would be in Euclidean space.
This can be made more quantitative, in order to characterize the precise value of the scalar curvature S at a point p of a Riemannian n-manifold
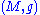.Namely, the ratio of the n-dimensional volume of a ball of radius ε in the manifold to that of a corresponding ball in
Euclidean space is given, for small ε, by
-
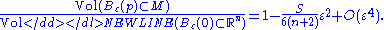
Thus, the second derivative of this ratio, evaluated at radius ε = 0, is exactly minus the scalar curvature divided by 3(n + 2).
Boundaries of these balls are (n-1) dimensional spheres with radii
; their hypersurface measures ("areas") satisfy the following equation:
-
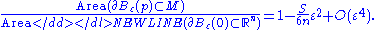
Surfaces
In two dimensions, scalar curvature is exactly twice the Gaussian curvatureGaussian curvatureIn differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
. For an embedded surface in Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, this means that
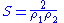
where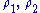
are principal radiiPrincipal curvatureIn differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
of the surface. For example, scalar curvature of a sphere with radius r is equal to 2/r2.
The 2-dimensional Riemann tensor has only one independent component and it can be easily expressed
in terms of the scalar curvature and metric area form. In any coordinate system, one thus has: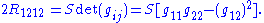
Space forms
A space formSpace formIn mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
is by definition a Riemannian manifold with constant sectional curvature. Space forms are locally isometric to one of the following types:- Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
: The Riemann tensor of an n-dimensional Euclidean space vanishes identically, so the scalar curvature does as well. - n-spheres: The sectional curvature of an n-sphere of radius r is K = 1/r2. Hence the scalar curvature is S = n(n−1)/r2.
- Hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
s: By the hyperboloid modelHyperboloid modelIn geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
, an n dimensional hyperbolic space can be identified with the subset of (n+1)-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
-
- The parameter r is a geometrical invariant of the hyperbolic space, and the sectional curvature is K = −1/r2. The scalar curvature is thus S = −n(n−1)/r2.
Traditional notation
Among those who use index notation for tensors, it is common to use the letter R to represent three different things:- the Riemann curvature tensorRiemann curvature tensorIn the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
:
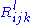or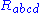 
- the Ricci tensor:
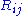
- the scalar curvature: R
These three are then distinguished from each other by their number of indices: the Riemann tensor has four indices, the Ricci tensor has two indices, and the Ricci scalar has zero indices. Those not using an index notation usually reserve R for the full Riemann curvature tensor.
See also
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Yamabe invariantYamabe invariantIn mathematics, in the field of differential geometry, the Yamabe invariant is a real number invariant associated to a smooth manifold that is preserved under diffeomorphisms. It was first written down independently by O. Kobayashi and R. Schoen and takes its name from H...
- Euclidean space
-
