Sectional curvature
Encyclopedia
In Riemannian geometry
, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds
. The sectional curvature K(σp) depends on a two-dimensional plane σp in the tangent space at p. It is the Gaussian curvature
of that section — the surface
which has the plane σp as a tangent plane at p, obtained from geodesic
s which start at p in the directions of σp (in other words, the image of σp under the exponential map
at p). The sectional curvature is a smooth real-valued function on the 2-Grassmannian
bundle
over the manifold.
The sectional curvature determines the curvature tensor
completely.
and two linearly independent tangent vectors at the same point, u and v, we can define
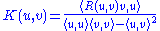
Here R is the Riemann curvature tensor
.
In particular, if u and v are orthonormal, then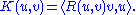
The sectional curvature in fact depends only on the 2-plane σp in the tangent space at p spanned by u and v. It is called the sectional curvature of the 2-plane σp, and is denoted K(σp).
s with constant sectional curvature are the most simple. These are called space form
s. By rescaling the metric there are three possible cases
The model manifolds for the three geometries are hyperbolic space
, Euclidean space
and a unit sphere. They are the only complete
, simply connected Riemannian manifolds of given sectional curvature. All other complete constant curvature manifolds are quotients of those by some group of isometries
.
If for each point in a connected Riemannian manifold (of dimension three or greater) the sectional curvature is independent of the tangent 2-plane, then the sectional curvature is in fact constant on the whole manifold.
affords a characterization of sectional curvature in terms of how "fat" geodesic triangles appear when compared to their Euclidean counterparts. The basic intuition is that, if a space is positively curved, then the edge of a triangle opposite some given vertex will tend to bend away from that vertex, whereas if a space is negatively curved, then the opposite edge of the triangle will tend to bend towards the vertex.
More precisely, let M be a complete
Riemannian manifold, and let xyz be a geodesic triangle in M (a triangle each of whose sides is a length-minimizing geodesic). Finally, let m be the midpoint of the geodesic xy. If M has non-negative curvature, then for all sufficiently small triangles
where d is the distance function on M. The case of equality holds precisely when the curvature of M vanishes, and the right-hand side represents the distance from a vertex to the opposite side of a geodesic triangle in Euclidean space having the same side-lengths as the triangle xyz. This makes precise the sense in which triangles are "fatter" in positively curved spaces. In non-positively curved spaces, the inequality goes the other way:
If tighter bounds on the sectional curvature are known, then this property generalizes to give a comparison theorem
between geodesic triangles in M and those in a suitable simply connected space form; see Toponogov's theorem
. Simple consequences of the version stated here are:
proved the Cartan–Hadamard theorem
: if M is a complete
manifold with non-positive sectional curvature, then its universal cover is diffeomorphic to a Euclidean space
. In particular, it is aspherical
: the homotopy groups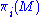
for i ≥ 2 are trivial. Therefore, the topological structure of a complete non-positively curved manifold is determined by its fundamental group
. Preissman's theorem
restricts the fundamental group of negatively curved compact manifolds.
implies that a complete non-compact non-negatively curved manifold is diffeomorphic to a normal bundle over a compact non-negatively curved manifold. As for compact positively curved manifolds, there are two classical results:
Moreover, there are relatively few examples of compact positively curved manifolds, leaving a lot of conjectures (e.g., the Hopf conjecture
on whether there is a metric of positive sectional curvature on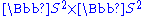
). The most typical way of constructing new examples is the following corollary from the O'Neill curvature formulas: if 
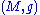is a Riemannian manifold admitting a free isometric action of a Lie group G, and M has positive sectional curvature on all 2-planes orthogonal to the orbits of G, then the manifold 
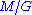with the quotient metric has positive sectional curvature. This fact allows one to construct the classical positively curved spaces, being spheres and projective spaces, as well as these examples :
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
. The sectional curvature K(σp) depends on a two-dimensional plane σp in the tangent space at p. It is the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of that section — the surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
which has the plane σp as a tangent plane at p, obtained from geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s which start at p in the directions of σp (in other words, the image of σp under the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
at p). The sectional curvature is a smooth real-valued function on the 2-Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over the manifold.
The sectional curvature determines the curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
completely.
Definition
Given a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and two linearly independent tangent vectors at the same point, u and v, we can define
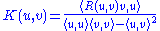
Here R is the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
In particular, if u and v are orthonormal, then
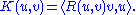
The sectional curvature in fact depends only on the 2-plane σp in the tangent space at p spanned by u and v. It is called the sectional curvature of the 2-plane σp, and is denoted K(σp).
Manifolds with constant sectional curvature
Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s with constant sectional curvature are the most simple. These are called space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
s. By rescaling the metric there are three possible cases
- negative curvature −1, hyperbolic geometryHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
- zero curvature, Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
- positive curvature +1, elliptic geometryElliptic geometryElliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
The model manifolds for the three geometries are hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and a unit sphere. They are the only complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, simply connected Riemannian manifolds of given sectional curvature. All other complete constant curvature manifolds are quotients of those by some group of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
If for each point in a connected Riemannian manifold (of dimension three or greater) the sectional curvature is independent of the tangent 2-plane, then the sectional curvature is in fact constant on the whole manifold.
Toponogov's theorem
Toponogov's theoremToponogov's theorem
In the mathematical field of Riemannian geometry, Toponogov's theorem is a triangle comparison theorem. It is one of a family of theorems that quantify the assertion that a pair of geodesics emanating from a point p spread apart more slowly in a region of high curvature than they would in a region...
affords a characterization of sectional curvature in terms of how "fat" geodesic triangles appear when compared to their Euclidean counterparts. The basic intuition is that, if a space is positively curved, then the edge of a triangle opposite some given vertex will tend to bend away from that vertex, whereas if a space is negatively curved, then the opposite edge of the triangle will tend to bend towards the vertex.
More precisely, let M be a complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
Riemannian manifold, and let xyz be a geodesic triangle in M (a triangle each of whose sides is a length-minimizing geodesic). Finally, let m be the midpoint of the geodesic xy. If M has non-negative curvature, then for all sufficiently small triangles
where d is the distance function on M. The case of equality holds precisely when the curvature of M vanishes, and the right-hand side represents the distance from a vertex to the opposite side of a geodesic triangle in Euclidean space having the same side-lengths as the triangle xyz. This makes precise the sense in which triangles are "fatter" in positively curved spaces. In non-positively curved spaces, the inequality goes the other way:
If tighter bounds on the sectional curvature are known, then this property generalizes to give a comparison theorem
Comparison theorem
A comparison theorem is any of a variety of theorems that compare properties of various mathematical objects.-Riemannian geometry:In Riemannian geometry it is a traditional name for a number of theorems that compare various metrics and provide various estimates in Riemannian geometry.*Rauch...
between geodesic triangles in M and those in a suitable simply connected space form; see Toponogov's theorem
Toponogov's theorem
In the mathematical field of Riemannian geometry, Toponogov's theorem is a triangle comparison theorem. It is one of a family of theorems that quantify the assertion that a pair of geodesics emanating from a point p spread apart more slowly in a region of high curvature than they would in a region...
. Simple consequences of the version stated here are:
- A complete Riemannian manifold has non-negative sectional curvature if and only if the function
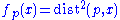is 1-concaveGlossary of Riemannian and metric geometryThis is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology....
for all points p. - A complete simply connected Riemannian manifold has non-positive sectional curvature if and only if the function
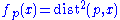is 1-convexGlossary of Riemannian and metric geometryThis is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology....
.
Manifolds with non-positive sectional curvature
In 1928, Élie CartanÉlie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
proved the Cartan–Hadamard theorem
Cartan–Hadamard theorem
The Cartan–Hadamard theorem is a statement in Riemannian geometry concerning the structure of complete Riemannian manifolds of non-positive sectional curvature. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space via the exponential map at any point...
: if M is a complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
manifold with non-positive sectional curvature, then its universal cover is diffeomorphic to a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In particular, it is aspherical
Aspherical space
In topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
: the homotopy groups
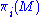for i ≥ 2 are trivial. Therefore, the topological structure of a complete non-positively curved manifold is determined by its fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. Preissman's theorem
Preissman's theorem
In Riemannian geometry, a field of mathematics, Preissman's theorem is a statement that restricts the possible topology of a negatively curved compact Riemannian manifold M...
restricts the fundamental group of negatively curved compact manifolds.
Manifolds with positive sectional curvature
Little is known about the structure of positively curved manifolds. The soul theoremSoul theorem
In mathematics, the soul theorem is a theorem of Riemannian geometry that largely reduces the study of complete manifolds of non-negative sectional curvature to that of the compact case. Cheeger and Gromoll proved the theorem in 1972 by generalizing a 1969 result of Gromoll and Meyer...
implies that a complete non-compact non-negatively curved manifold is diffeomorphic to a normal bundle over a compact non-negatively curved manifold. As for compact positively curved manifolds, there are two classical results:
- It follows from the Myers theorem that the fundamental group of such manifold is finite.
- It follows from the Synge theorem that the fundamental group of such manifold in even dimensions is 0, if orientable and
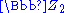otherwise. In odd dimensions a positively curved manifold is always orientable.
Moreover, there are relatively few examples of compact positively curved manifolds, leaving a lot of conjectures (e.g., the Hopf conjecture
Hopf conjecture
In mathematics, Hopf conjecture may refer to one of several conjectural statements from differential geometry and topology attributed to Heinz Hopf.- Positively curved Riemannian manifolds :...
on whether there is a metric of positive sectional curvature on
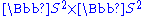). The most typical way of constructing new examples is the following corollary from the O'Neill curvature formulas: if 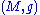is a Riemannian manifold admitting a free isometric action of a Lie group G, and M has positive sectional curvature on all 2-planes orthogonal to the orbits of G, then the manifold 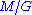with the quotient metric has positive sectional curvature. This fact allows one to construct the classical positively curved spaces, being spheres and projective spaces, as well as these examples :- The Berger spaces
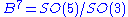and 
.
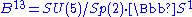- The Wallach spaces (or the homogeneous flag manifolds):
, 
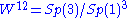and 
.
- The Aloff–Wallach spaces
.
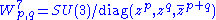- The Eschenburg spaces
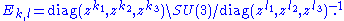
- The Bazaikin spaces
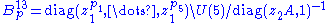, where 
.
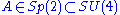See also
- Riemann curvature tensorRiemann curvature tensorIn the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
- curvature of Riemannian manifoldsCurvature of Riemannian manifoldsIn mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
- curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...