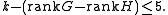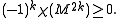In mathematics, Hopf conjecture may refer to one of several conjectural statements from differential geometry and topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 attributed to Heinz Hopf

Heinz Hopf

Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...

.

Positively curved Riemannian manifolds

A compact, even-dimensional Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

 with positive sectional curvature

Sectional curvature

In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...

 has positive Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

.

For surfaces

Differential geometry of surfaces

In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....

, this follows from the Gauss–Bonnet theorem

Gauss–Bonnet theorem

The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...

. For four-dimensional manifolds, this follows from the finiteness of the fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

 and the Poincaré duality

Poincaré duality

In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...

. The conjecture has been proved for manifolds of dimension 4k+2 or 4k+4 admitting an isometric torus action of a k-dimensional torus and for manifolds M admitting an isometric action of a compact Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

 G with principal isotropy subgroup H and cohomogeneity k such that

In a related conjecture, "positive" is replaced with "nonnegative".

Riemannian symmetric spaces

A compact symmetric space

Symmetric space

A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...

 of rank greater than one cannot carry a Riemannian metric of positive sectional curvature.

In particular, the four-dimensional manifold S²×S² should admit no Riemannian metric with positive sectional curvature.

Aspherical manifolds

Suppose M²k is a closed, aspherical manifold of even dimension. Then its Euler characteristic satisfies the inequality

This topological version of Hopf conjecture for Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

s is due to William Thurston

William Thurston

William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...

. Ruth Charney and Mike Davis conjectured that the same inequality holds for a nonpositively curved piecewise Euclidean (PE) manifold.