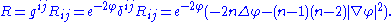List of formulas in Riemannian geometry
Encyclopedia
Christoffel symbols, covariant derivative
In a smooth coordinate chart, the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
are given by:

Here
 is the inverse
is the inverseInverse
Inverse may refer to:* Inverse , a type of immediate inference from a conditional sentence* Inverse , a program for solving inverse and optimization problems...
matrix to the metric tensor
 . In other words,
. In other words,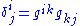
and thus
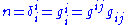
is the dimension of the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
Christoffel symbols satisfy the symmetry relation
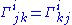
which is equivalent to the torsion-freeness of the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
.
The contracting relations on the Christoffel symbols are given by
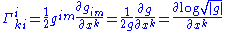
and

where |g| is the absolute value of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor
 . These are useful when dealing with divergences and Laplacians (see below).
. These are useful when dealing with divergences and Laplacians (see below).The covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
with components
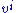 is given by:
is given by: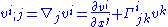
and similarly the covariant derivative of a
 -tensor field
-tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
with components
 is given by:
is given by: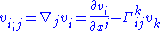
For a
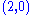 -tensor field
-tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
with components
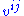 this becomes
this becomes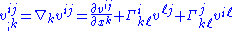
and likewise for tensors with more indices.
The covariant derivative of a function (scalar)
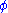 is just its usual differential:
is just its usual differential: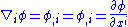
Because the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
is metric-compatible, the covariant derivatives of metrics vanish,
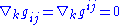
The geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
 starting at the origin with initial speed
starting at the origin with initial speed 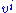 has Taylor expansion in the chart:
has Taylor expansion in the chart: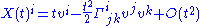
Riemann curvature tensor
If one defines the curvature operatorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
as
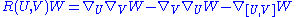
and the coordinate components of the
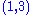 -Riemann curvature tensor
-Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
by
 , then these components are given by:
, then these components are given by:
where n denotes the dimension of the manifold. Lowering indices with
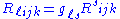 one gets
one gets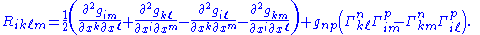
The symmetries of the tensor are
 and
and 
That is, it is symmetric in the exchange of the first and last pair of indices, and antisymmetric in the flipping of a pair.
The cyclic permutation sum (sometimes called first Bianchi identity) is
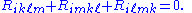
The (second) Bianchi identity is

that is,

which amounts to a cyclic permutation sum of the last three indices, leaving the first two fixed.
Ricci and scalar curvatures
Ricci and scalar curvatures are contractions of the Riemann tensor. They simplify the Riemann tensor, but contain less information.The Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
tensor is essentially the unique nontrivial way of contracting the Riemann tensor:

The Ricci tensor
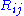 is symmetric.
is symmetric.By the contracting relations on the Christoffel symbols, we have
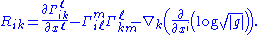
The scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
is the trace of the Ricci curvature,
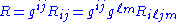 .
.The "gradient" of the scalar curvature follows from the Bianchi identity (proof):

that is,
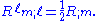
Einstein tensor
The Einstein tensorEinstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
Gab is defined in terms of the Ricci tensor Rab and the Ricci scalar R,
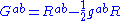
where g is the metric tensor.
The Einstein tensor is symmetric, with a vanishing divergence (proof) which is due to the Bianchi identity:
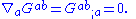
Weyl tensor
The Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
is given by

where
 denotes the dimension of the Riemannian manifold.
denotes the dimension of the Riemannian manifold.Gradient, divergence, Laplace–Beltrami operator
The gradient of a function is obtained by raising the index of the differential
is obtained by raising the index of the differential  , that is:
, that is: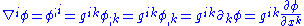
The divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of a vector field with components
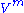 is
is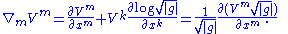
The Laplace–Beltrami operator acting on a function
 is given by the divergence of the gradient:
is given by the divergence of the gradient: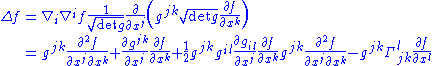
The divergence of an antisymmetric tensor field of type
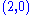 simplifies to
simplifies to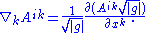
Kulkarni–Nomizu product
The Kulkarni–Nomizu product is an important tool for constructing new tensors from existing tensors on a Riemannian manifold. Let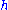 and
and  be symmetric covariant 2-tensors. In coordinates,
be symmetric covariant 2-tensors. In coordinates,
Then we can multiply these in a sense to get a new covariant 4-tensor, which we denote
 . The defining formula is
. The defining formula is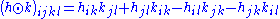
Often the Kulkarni–Nomizu product is denoted by a circle with a wedge that points up inside it. However, we will use
 instead throughout this article. Clearly, the product satisfies
instead throughout this article. Clearly, the product satisfies
Let us use the Kulkarni–Nomizu product to define some curvature quantities.
Weyl tensor
The Weyl tensor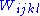 is defined by the formula
is defined by the formula
Each of the summands on the righthand side have remarkable properties. Recall the first (algebraic) Bianchi identity that a tensor
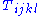 can satisfy:
can satisfy: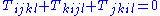
Not only the Riemann curvature tensor on the left, but also the three summands on the right satisfy this Bianchi identity. Furthermore, the first factor in the second summand has trace zero. The Weyl tensor is a symmetric product of alternating 2-forms,

just like the Riemann tensor. Moreover, taking the trace over any two indices gives zero,
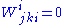
In fact, any tensor that satisfies the first Bianchi identity can be written as a sum of three terms. The first, a scalar multiple of
 . The second, as
. The second, as 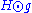 where
where  is a symmetric trace-free 2-tensor. The third, a symmetric product of alternating two-forms which is totally traceless, like the Weyl tensor described above.
is a symmetric trace-free 2-tensor. The third, a symmetric product of alternating two-forms which is totally traceless, like the Weyl tensor described above.The most remarkable property of the Weyl tensor, though, is that it vanishes (
 )if and only if a manifold
)if and only if a manifold  of dimension
of dimension  is locally conformally flat. In other words,
is locally conformally flat. In other words,  can be covered by coordinate systems in which the metric
can be covered by coordinate systems in which the metric 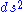 satisfies
satisfies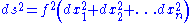
This is essentially because
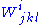 is invariant under conformal changes.
is invariant under conformal changes.In an inertial frame
An orthonormal inertial frame is a coordinate chart such that, at the origin, one has the relations and
and  (but these may not hold at other points in the frame).
(but these may not hold at other points in the frame).In such a frame, the expression for several operators is simpler. Note that the formulae given below are valid at the origin of the frame only.
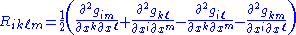
Under a conformal change
Let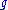 be a Riemannian metric on a smooth manifold
be a Riemannian metric on a smooth manifold  , and
, and  a smooth real-valued function on
a smooth real-valued function on  . Then
. Then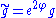
is also a Riemannian metric on
 . We say that
. We say that  is conformal to
is conformal to  . Evidently, conformality of metrics is an equivalence relation. Here are some formulas for conformal changes in tensors associated with the metric. (Quantities marked with a tilde will be associated with
. Evidently, conformality of metrics is an equivalence relation. Here are some formulas for conformal changes in tensors associated with the metric. (Quantities marked with a tilde will be associated with  , while those unmarked with such will be associated with
, while those unmarked with such will be associated with  .)
.)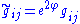
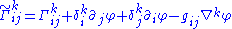
Note that the difference between the Christoffel symbols of two different metrics always form the components of a tensor.
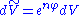
Here
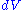 is the Riemannian volume element.
is the Riemannian volume element.
Here
 is the Kulkarni-Nomizu product defined earlier in this article. The symbol
is the Kulkarni-Nomizu product defined earlier in this article. The symbol 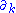 denotes partial derivative, while
denotes partial derivative, while 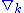 denotes covariant derivative.
denotes covariant derivative.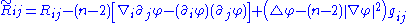
Beware that here the Laplacian
 is minus the trace of the Hessian on functions,
is minus the trace of the Hessian on functions,
Thus the operator
 is elliptic because the metric
is elliptic because the metric  is Riemannian.
is Riemannian.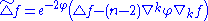

If the dimension
 , then this simplifies to
, then this simplifies to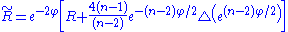
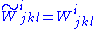
We see that the (3,1) Weyl tensor is invariant under conformal changes.
Let
 be a differential
be a differential 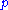 -form. Let
-form. Let  be the Hodge star, and
be the Hodge star, and  the codifferential. Under a conformal change, these satisfy
the codifferential. Under a conformal change, these satisfy
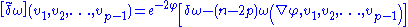
Conformally flat manifolds
WARNING: THE FORMULAS BELOW ARE UNCHECKED AND COULD VERY WELL BE WRONGThe setting where the metric takes the form
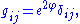
where
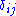 is the standard Euclidean metric, is particularly simple. These manifolds are called conformally flat. In what follows, all the partial derivatives
is the standard Euclidean metric, is particularly simple. These manifolds are called conformally flat. In what follows, all the partial derivatives  and the Laplacian
and the Laplacian  are with respect to the Euclidean metric.
are with respect to the Euclidean metric.The Christoffel symbols are


for
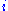 ,
, 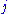 , and
, and 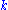 all distinct.
all distinct.In this setting, the Ricci tensor takes the form
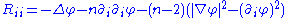

for
 and
and  distinct. The scalar curvature thus is
distinct. The scalar curvature thus is