
Lie bracket of vector fields
Encyclopedia
- See Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
for more on the definition of the Lie bracket and Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
for the derivation
In the mathematical field of differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
which assigns, to any two vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s X and Y on a smooth manifold M, a third vector field denoted [X, Y]. It is the specialization of the Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
to the case of Lie differentiation of a vector field. Indeed,
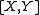 equals the Lie derivative
equals the Lie derivative 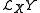 .
.It plays an important role in differential geometry and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, and is also fundamental in the geometric theory for nonlinear control systems ' onMouseout='HidePop("54326")' href="/topics/Nonholonomic_system">nonholonomic system
Nonholonomic system
A nonholonomic system in physics and mathematics is a system whose state depends on the path taken to achieve it. Such a system is described by a set of parameters subject to differential constraints, such that when the system evolves along a path in its parameter space but finally returns to the...
s; , feedback linearization
Feedback linearization
Feedback linearization is a common approach used in controlling nonlinear systems. The approach involves coming up with a transformation of the nonlinear system into an equivalent linear system through a change of variables and a suitable control input...
).
A generalization of the Lie bracket (to vector-valued differential forms) is the Frölicher–Nijenhuis bracket.
Definition
Each vector field X on a smooth manifold Mmay be regarded as a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
acting on smooth
functions on M. Indeed, for each p,
the vector X(p) is a derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
on the smooth
functions defined near p.
The Jacobi–Lie bracket or simply Lie bracket,
[X,Y], of two vector fields
X and Y is the differential operator defined by
One can show that, at each point, this operator
is a derivation, and hence the Lie bracket is a vector field.
To make the connection to the Lie derivative, let
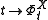 be the 1-parameter group of diffeomorphisms (or
be the 1-parameter group of diffeomorphisms (orflow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
)
generated by the vector field
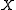 .
.The differential
Push forward
Suppose that φ : M → N is a smooth map between smooth manifolds; then the differential of φ at a point x is, in some sense, the best linear approximation of φ near x. It can be viewed as a generalization of the total derivative of ordinary calculus...
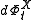 of each diffeomorphism
of each diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
maps the vector field Y to a new vector field
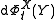 . To pull-back the vector
. To pull-back the vectorfield one applies the differential of the inverse,
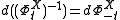 .
.The Lie bracket is defined by
In particular,
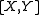 is the
is theLie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of the vector field
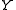 with respect
with respectto
 . Conceptually, the Lie bracket is the derivative
. Conceptually, the Lie bracket is the derivativeof
 in the `direction' generated by
in the `direction' generated by 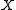 .
.Though neither definition of the Lie bracket depends
on a choice of coordinates, in practice one often wants to compute
the bracket with respect to a coordinate system.
Let
 be a set of local coordinate functions,
be a set of local coordinate functions,and let

denote the associated local frame. Then
(Here we use the Einstein summation convention)
Properties
The Lie bracket of vector fields equips the real vector space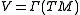 (i.e., smooth sections of the tangent bundle of
(i.e., smooth sections of the tangent bundle of  ) with the structure of a Lie algebra
) with the structure of a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, i.e., [·,·] is a map from
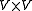 to
to  with the following properties
with the following properties
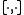 is R-bilinear
is R-bilinear
 This is the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
This is the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.- For functions f and g we have
-
-
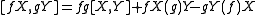 .
.
-
These three properties together also define a Lie algebroid
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
. Note that the infinite dimensional Lie algebra has nice topological properties.
An immediate consequence of the second property is that
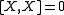 for any
for any 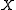 .
.The name commutator is used because the Lie bracket is the commutator of the vector fields considered as
differentiable operators. We also have the following fact:
Theorem:
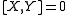 iff the commutator of flows
iff the commutator of flows 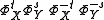 is
isa closed loop. Alternatively the lift of the flows on the universal covering commute
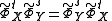 .
.Examples
For a Lie group, the Lie algebra is tangent space at the identity, which can be identified with the left invariant vector fields. The Lie bracket of the Lie algebra is then the Lie bracket of the left invariant vector fields, which is also left invariant.For a matrix Lie group, smooth vector fields can be locally represented in the corresponding Lie algebra. Since the Lie algebra associated with a Lie group is isomorphic to the group's tangent space at the identity, elements of the Lie algebra of a matrix Lie group are also matrices. Hence the Jacobi–Lie bracket corresponds to the usual commutator for a matrix group:
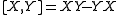
where juxtaposition indicates matrix multiplication.




