
Push forward
Encyclopedia
Suppose that φ : M → N is a smooth map between smooth manifolds; then the differential of φ at a point x is, in some sense, the best linear approximation
of φ near x. It can be viewed as a generalization of the total derivative
of ordinary calculus. Explicitly, it is a linear map from the tangent space
of M at x to the tangent space of N at φ(x). Hence it can be used to push tangent vectors on M forward to tangent vectors on N.
The differential of a map φ is also called, by various authors, the derivative or total derivative of φ, and is sometimes itself called the pushforward.
representation of the total derivative
of φ at x, which is a linear map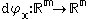
from Rm to Rn.
We wish to generalize this to the case that φ is a smooth function between any smooth manifolds M and N.
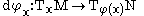
from the tangent space
of M at x to the tangent space of N at φ(x). The application of dφx to a tangent vector X is sometimes called the pushforward of X by φ. The exact definition of this pushforward depends on the definition one uses for tangent vectors (for the various definitions see tangent space
).
If one defines tangent vectors as equivalence classes of curves through x then the differential is given by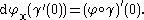
Here γ is a curve in M with γ(0) = x. In other words, the pushforward of the tangent vector to the curve γ at 0 is just the tangent vector to the curve φ∘γ at 0.
Alternatively, if tangent vectors are defined as derivations
acting on smooth real-valued functions, then the differential is given by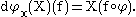
Here X ∈ TxM, therefore X is a derivation defined on M and f is a smooth real-valued function on N. By definition, the pushforward of X at a given x in M is in Tφ(x)N and therefore itself is a derivation.
After choosing charts around x and φ(x), F is locally determined by a smooth map
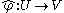
between open sets of Rm and Rn, and dφx has representation (at x)
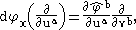
in the Einstein summation notation, where the partial derivatives are evaluated at the point in U corresponding to x in the given chart.
Extending by linearity gives the following matrix
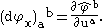
Thus the differential is a linear transformation, between tangent spaces, associated to the smooth map φ at each point. Therefore, in some chosen local coordinates, it is represented by the Jacobian of the corresponding smooth map from Rm to Rn. In general the differential need not be invertible. If φ is a local diffeomorphism
, then the pushforward at x is invertible and its inverse gives the pullback of Tφ(x)N.
The differential is frequently expressed using a variety of other notations such as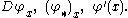
It follows from the definition that the differential of a composite
is the composite of the differentials (i.e., functor
ial behaviour). This is the chain rule for smooth maps.
Also, the differential of a local diffeomorphism
is a linear isomorphism of tangent spaces.
(in fact a vector bundle homomorphism) from the tangent bundle
of M to the tangent bundle of N, denoted by dφ or φ*, which fits into the following commutative diagram
:
where πM and πN denote the bundle projections of the tangent bundles of M and N respectively.
Equivalently (see bundle map
), φ* = dφ is a bundle map from TM to the pullback bundle
φ*TN over M, which may in turn be viewed as a section
of the vector bundle
Hom(TM,φ*TN) over M.
X on M, it is not usually possible to define a pushforward of X by φ as a vector field on N. For example, if the map φ is not surjective, there is no natural way to define such a pushforward outside of the image of φ. Also, if φ is not injective there may be more than one choice of pushforward at a given point. Nevertheless, one can make this difficulty precise, using the notion of a vector field along a map.
A section
of φ*TN over M is called a vector field along φ. For example, if M is a submanifold of N and φ is the inclusion, then a vector field along φ is just a section of the tangent bundle of N along M; in particular, a vector field on M defines such a section via the inclusion of TM inside TN. This idea generalizes to arbitrary smooth maps.
Suppose that X is a vector field on M, i.e., a section of TM. Then, applying the differential pointwise to X yields the pushforward φ*X, which is a vector field along φ, i.e., a section of φ*TN over M.
Any vector field Y on N defines a pullback section
φ*Y of φ*TN with (φ*Y)x = Yφ(x). A vector field X on M and a vector field Y on N are said to be φ-related if φ*X = φ*Y as vector fields along φ. In other words, for all x in M, dφx(X)=Yφ(x).
In some situations, given a X vector field on M, there is a unique vector field Y on M which is φ-related to X. This is true in particular when φ is a diffeomorphism
. In this case, the pushforward defines a vector field Y on N, given by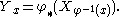
A more general situation arises when φ is surjective (for example the bundle projection
of a fiber bundle). Then a vector field X on M is said to be projectable if for all y in N, dφx(Xx) is independent of the choice of x in φ−1({y}). This is precisely the condition that guarantees that a pushforward of X, as a vector field on N, is well defined.
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
of φ near x. It can be viewed as a generalization of the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of ordinary calculus. Explicitly, it is a linear map from the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of M at x to the tangent space of N at φ(x). Hence it can be used to push tangent vectors on M forward to tangent vectors on N.
The differential of a map φ is also called, by various authors, the derivative or total derivative of φ, and is sometimes itself called the pushforward.
Motivation
Let φ:U→V be a smooth map from an open subset U of Rm to an open subset V of Rn. For any point x in U, the Jacobian of φ at x (with respect to the standard coordinates) is the matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
representation of the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of φ at x, which is a linear map
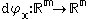
from Rm to Rn.
We wish to generalize this to the case that φ is a smooth function between any smooth manifolds M and N.
The differential of a smooth map
Let φ : M → N be a smooth map of smooth manifolds. Given some x ∈ M, the differential (or (total) derivative) of φ at x is a linear map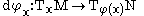
from the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of M at x to the tangent space of N at φ(x). The application of dφx to a tangent vector X is sometimes called the pushforward of X by φ. The exact definition of this pushforward depends on the definition one uses for tangent vectors (for the various definitions see tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
).
If one defines tangent vectors as equivalence classes of curves through x then the differential is given by
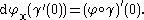
Here γ is a curve in M with γ(0) = x. In other words, the pushforward of the tangent vector to the curve γ at 0 is just the tangent vector to the curve φ∘γ at 0.
Alternatively, if tangent vectors are defined as derivations
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
acting on smooth real-valued functions, then the differential is given by
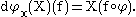
Here X ∈ TxM, therefore X is a derivation defined on M and f is a smooth real-valued function on N. By definition, the pushforward of X at a given x in M is in Tφ(x)N and therefore itself is a derivation.
After choosing charts around x and φ(x), F is locally determined by a smooth map
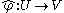
between open sets of Rm and Rn, and dφx has representation (at x)
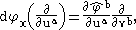
in the Einstein summation notation, where the partial derivatives are evaluated at the point in U corresponding to x in the given chart.
Extending by linearity gives the following matrix
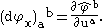
Thus the differential is a linear transformation, between tangent spaces, associated to the smooth map φ at each point. Therefore, in some chosen local coordinates, it is represented by the Jacobian of the corresponding smooth map from Rm to Rn. In general the differential need not be invertible. If φ is a local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
, then the pushforward at x is invertible and its inverse gives the pullback of Tφ(x)N.
The differential is frequently expressed using a variety of other notations such as
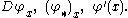
It follows from the definition that the differential of a composite
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
is the composite of the differentials (i.e., functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial behaviour). This is the chain rule for smooth maps.
Also, the differential of a local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
is a linear isomorphism of tangent spaces.
The differential on the tangent bundle
The differential of a smooth map φ induces, in an obvious manner, a bundle mapBundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
(in fact a vector bundle homomorphism) from the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M to the tangent bundle of N, denoted by dφ or φ*, which fits into the following commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
where πM and πN denote the bundle projections of the tangent bundles of M and N respectively.
Equivalently (see bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
), φ* = dφ is a bundle map from TM to the pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
φ*TN over M, which may in turn be viewed as a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
Hom(TM,φ*TN) over M.
Pushforward of vector fields
Given a smooth map φ:M→N and a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X on M, it is not usually possible to define a pushforward of X by φ as a vector field on N. For example, if the map φ is not surjective, there is no natural way to define such a pushforward outside of the image of φ. Also, if φ is not injective there may be more than one choice of pushforward at a given point. Nevertheless, one can make this difficulty precise, using the notion of a vector field along a map.
A section
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of φ*TN over M is called a vector field along φ. For example, if M is a submanifold of N and φ is the inclusion, then a vector field along φ is just a section of the tangent bundle of N along M; in particular, a vector field on M defines such a section via the inclusion of TM inside TN. This idea generalizes to arbitrary smooth maps.
Suppose that X is a vector field on M, i.e., a section of TM. Then, applying the differential pointwise to X yields the pushforward φ*X, which is a vector field along φ, i.e., a section of φ*TN over M.
Any vector field Y on N defines a pullback section
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
φ*Y of φ*TN with (φ*Y)x = Yφ(x). A vector field X on M and a vector field Y on N are said to be φ-related if φ*X = φ*Y as vector fields along φ. In other words, for all x in M, dφx(X)=Yφ(x).
In some situations, given a X vector field on M, there is a unique vector field Y on M which is φ-related to X. This is true in particular when φ is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. In this case, the pushforward defines a vector field Y on N, given by
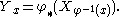
A more general situation arises when φ is surjective (for example the bundle projection
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of a fiber bundle). Then a vector field X on M is said to be projectable if for all y in N, dφx(Xx) is independent of the choice of x in φ−1({y}). This is precisely the condition that guarantees that a pushforward of X, as a vector field on N, is well defined.

