
Levi-Civita parallelogramoid
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space
Curved space
Curved space often refers to a spatial geometry which is not “flat” where a flat space is described by Euclidean geometry. Curved spaces can generally be described by Riemannian geometry though some simple cases can be described in other ways. Curved spaces play an essential role in General...
. It is named for its discoverer, Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
. It generalizes a parallelogram in that the sides AA′ and BB′ are parallel (via parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
) and the same length, but the last side A′B′ will not in general be parallel to or the same length as the side AB, though it will be straight (a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
).
A parallelogram in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
can be constructed as follows:
- Start with a straight line segment AB and another straight line segment AA′.
- Slide the segment AA′ along AB to the endpoint B, keeping the angle with AB constant, and remaining in the same plane as the points A, A′, and B.
- Label the endpoint of the resulting segment B′ so that the segment is BB′.
- Draw a straight line A′B′.
In a curved space, such as a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or more generally any manifold equipped with an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, the notion of "straight line" generalizes to that of a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
. In a suitable neighborhood (such as a ball in a normal coordinate system
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
), any two points can be joined by a geodesic. The idea of sliding the one straight line along the other gives way to the more general notion of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
. Thus, assuming either that the manifold is complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, or that the construction is taking place in a suitable neighborhood, the steps to producing a Levi-Civita parallelogram are:
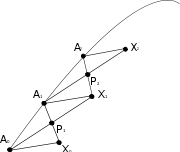
- Start with a geodesic AB and another geodesic AA′. These geodesics are assumed to be parameterized by their arclength in the case of a Riemannian manifold, or to carry a choice of affine parameter in the general case of an affine connection.
- "Slide" (parallel transportParallel transportIn geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
) the tangent vectorTangent vectorA tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
of AA′ from A to B. - The resulting tangent vector at B generates a geodesic via the exponential mapExponential mapIn differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
. Label the endpoint of this geodesic by B′, and the geodesic itself BB′. - Connect the points A′ and B′ by the geodesic A′B′.
The length of this last geodesic constructed connecting the remaining points A′B′ may in general be different than the length of the base AB. This difference is measured by the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. To state the relationship precisely, let AA′ be the exponential of a tangent vector X at A, and AB the exponential of a tangent vector Y at A. Then
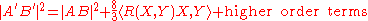
where terms of higher order in the length of the sides of the parallelogram have been suppressed.
Related concepts
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
can be discretely approximated by Schild's ladder
Schild's ladder
In the theory of general relativity, and differential geometry more generally, Schild's ladder is a first-order method for approximating parallel transport of a vector along a curve using only affinely parametrized geodesics...
, which approximates Levi-Civita parallelogramoids by approximate parallelograms.

